Question

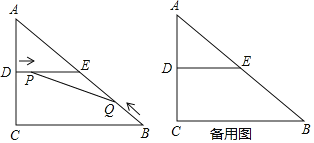
【题目】如图，在平面直角坐标系中，直线：与轴，轴分别交于，两点，且点，点在轴正半轴上运动，过点作平行于轴的直线．

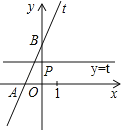
（1）求的值和点的坐标；

（2）当时，直线与直线交于点，反比例函数的图象经过点，求反比例函数的解析式；

（3）当时，若直线与直线和（2）反比例函数的图象分别交于点，，当间距离大于等于2时，求的取值范围．

Answer 1

【答案】（1），；（2）；的取值范围是：．

【解析】

（1）把代入得出的值，进而得出点坐标；

（2）当时，将代入，进而得出的值，求出点坐标得出反比例函数的解析式；

（3）可得，当向下运动但是不超过轴时，符合要求，进而得出的取值范围．

解：（1）∵直线： 经过点，

∴，

∴，

∴；

（2）当时，将代入，

得，，

∴代入得，，

∴；

（3）当时，即，而，

如图，，当向下运动但是不超过轴时，符合要求，

∴的取值范围是：．