题目内容
(1)P(0,1)向上平移3个单位后的坐标是(2)直线y=-2x+1向左平移3个单位后的解析式是
(3)已知P(0,1)、A(2,3),在x轴上求一点B,使BP+BA的值最小.
分析:(1)根据坐标与图形平移的规律,把P纵坐标加上3后即可得到平移后的坐标;把直线方程右边加上3即可得到平移后的直线解析式;
(2)根据图形平移规律,给自变量x加上3,化简后即可得到平移后的解析式;
(3)作出点P关于x轴的对称点P′连接AP′,与x轴的交于点B,根据两点之间线段最短,得到此时的点B满足BP+BA的值最小,设出直线AP′的解析式,把A和P′的坐标代入设出的解析式中即可确定出直线AP′的解析式,然后由点B是直线与x轴的交点,令y=0求出x的值,从而得到点B的坐标.
(2)根据图形平移规律,给自变量x加上3,化简后即可得到平移后的解析式;
(3)作出点P关于x轴的对称点P′连接AP′,与x轴的交于点B,根据两点之间线段最短,得到此时的点B满足BP+BA的值最小,设出直线AP′的解析式,把A和P′的坐标代入设出的解析式中即可确定出直线AP′的解析式,然后由点B是直线与x轴的交点,令y=0求出x的值,从而得到点B的坐标.
解答: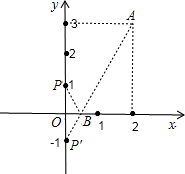 解:(1)P(0,1)向上平移3个单位后的坐标是(0,1+3),即(0,4);
解:(1)P(0,1)向上平移3个单位后的坐标是(0,1+3),即(0,4);
直线y=-2x+1向上平移3个单位后的解析式是y=-2x+1+3,即y=-2x+4;
(2)直线y=-2x+1向左平移3个单位后的解析式是y=-2(x+3)+1,即y=-2x-5;
(3)根据题意画出图形,如图所示:
找出点P关于x轴的对称点P′,连接AP′于x轴交于点B,连接PB,
此时PB=P′B,PB+BA=P′B+BA=AP′最短.
设直线AP′的解析式为y=kx+b,
把P′(0,-1)和A(2,3)代入得:
,
解得
,
故直线AP′的解析式为y=2x-1,令y=0,
解得x=
,
则点B坐标为(
,0).
 解:(1)P(0,1)向上平移3个单位后的坐标是(0,1+3),即(0,4);
解:(1)P(0,1)向上平移3个单位后的坐标是(0,1+3),即(0,4);直线y=-2x+1向上平移3个单位后的解析式是y=-2x+1+3,即y=-2x+4;
(2)直线y=-2x+1向左平移3个单位后的解析式是y=-2(x+3)+1,即y=-2x-5;
(3)根据题意画出图形,如图所示:
找出点P关于x轴的对称点P′,连接AP′于x轴交于点B,连接PB,
此时PB=P′B,PB+BA=P′B+BA=AP′最短.
设直线AP′的解析式为y=kx+b,
把P′(0,-1)和A(2,3)代入得:
|
解得
|
故直线AP′的解析式为y=2x-1,令y=0,
解得x=
| 1 |
| 2 |
则点B坐标为(
| 1 |
| 2 |
点评:此题考查学生掌握平移规律:上加下减,左加右减.注意上下是对一点的纵坐标或函数值而言,左右平移是对一点的横坐标或自变量而言.同时考查学生会利用对称性解决最短路线的问题.

练习册系列答案
相关题目

 20、岳飞是我国古代宋朝的民族英雄,曾任通泰镇抚史、兼泰州知州、据说在泰州抗击金兵期间,有一次曾向将领们讲了如下一个布阵图,如图4是一座城池,在城池的四周设了八个哨所,一共由24个卫士把守,按直线算,每边都有11个人,后来由于军情发生变化,连续四次给哨所增添兵力,每次增加4人,但要求在增加人员后,仍然保持每边11个人把守、请问,兵力应如何调整?
20、岳飞是我国古代宋朝的民族英雄,曾任通泰镇抚史、兼泰州知州、据说在泰州抗击金兵期间,有一次曾向将领们讲了如下一个布阵图,如图4是一座城池,在城池的四周设了八个哨所,一共由24个卫士把守,按直线算,每边都有11个人,后来由于军情发生变化,连续四次给哨所增添兵力,每次增加4人,但要求在增加人员后,仍然保持每边11个人把守、请问,兵力应如何调整?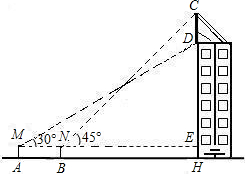 留一位小数)
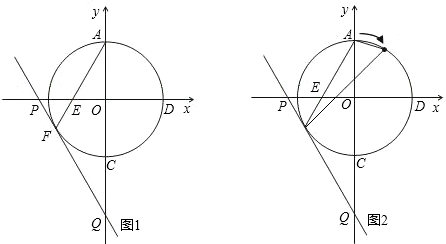
留一位小数) 9、如图,8×8方格纸上的两条对称轴EF,MN相交于中心点O,对△ABC分别作下列变换:
9、如图,8×8方格纸上的两条对称轴EF,MN相交于中心点O,对△ABC分别作下列变换: