题目内容
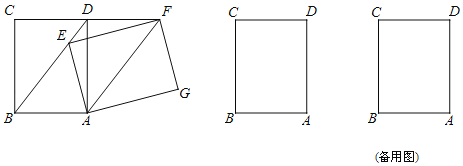
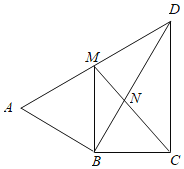
【题目】如图,![]() ,
,![]() 平分
平分![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,若
,若![]() ,
,![]() ,求
,求![]() ,
,![]() 的长.
的长.
【答案】BD=![]() ,DN=
,DN=![]()
【解析】
由平行线的性质可证∠MBD=∠BDC,即可证AM=MD=MB=4,由BD2=ADCD可得BD长,再由勾股定理可求MC的长,通过证明△MNB∽△CND,可得![]() ,即可求DN的长.
,即可求DN的长.
解:∵BM∥CD
∴∠MBD=∠BDC
∴∠ADB=∠MBD,且∠ABD=90°
∴BM=MD,∠MAB=∠MBA
∴BM=MD=AM=4
∵![]() 平分
平分![]() ,
,
∴∠ADB=∠CDB,
∵![]() ,
,
∴△ABD∽△BCD,
∴BD2=ADCD,
∵ CD=6,AD=8,
∴BD2=48,
即BD=![]() ,
,
∴BC2=BD2-CD2=12
∴MC2=MB2+BC2=28
∴MC=![]() ,
,
∵BM∥CD
∴△MNB∽△CND,
∴![]() ,且BD=
,且BD=![]() ,
,
∴设DN=x,
则有![]() ,
,
解得x=![]() ,
,
即DN=![]() .
.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
【题目】为提升学生的艺术素养,某校计划开设四门选修课程:声乐、舞蹈、书法、摄影.要求每名学生必须选修且只能选修一门课程,为保证计划的有效实施,学校随机对部分学生进行了一次调查,并将调査结果绘制成如下不完整的统计表和统计图.
学生选修课程统计表
课程 | 人数 | 所占百分比 |
声乐 | 14 |
|
舞蹈 | 8 |
|
书法 | 16 |
|
摄影 |
|
|
合计 |
|
|

根据以上信息,解答下列问题:
(1)![]() ,
,![]() .
.
(2)求出![]() 的值并补全条形统计图.
的值并补全条形统计图.
(3)该校有1500名学生,请你估计选修“声乐”课程的学生有多少名.
(4)七(1)班和七(2)班各有2人选修“舞蹈”课程且有舞蹈基础,学校准备从这4人中随机抽取2人编排“舞蹈”在开班仪式上表演,请用列表法或画树状图的方法求所抽取的2人恰好来自同一个班级的概率.