题目内容
【题目】如图,等边![]() 中,
中, ![]() 是
是![]() 的角平分线,
的角平分线, ![]() 为
为![]() 上一点,以
上一点,以![]() 为一边且在
为一边且在![]() 下方作等边
下方作等边![]() ,连接
,连接![]() .
.
(![]() )求证:
)求证: ![]() ≌
≌![]() .
.
(![]() )延长
)延长![]() 至
至![]() ,
, ![]() 为
为![]() 上一点,连接
上一点,连接![]() 、
、![]() 使
使![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
【答案】(![]() )证明见解析;(
)证明见解析;(![]() )PQ=8.
)PQ=8.
【解析】试题分析:
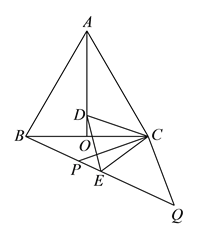
(1)由△ABC、△DCE都是等边三角形可得:AC=BC、CD=CE,∠ACB=∠DCE=60°,从而可得∠ACD=∠BCE,这样由“SAS”即可证得:△ACD≌△BCE;
(2)由等边△ABC中,AO平分∠BAC可得∠CAD=![]() ∠BAC=30°,结合△ACD≌△BCE可得∠CBE=30°;过点C作CH⊥BQ于点H,由此可得CH=
∠BAC=30°,结合△ACD≌△BCE可得∠CBE=30°;过点C作CH⊥BQ于点H,由此可得CH=![]() BC=3,在Rt△CHQ中,由勾股定理可得HQ=4,结合CP=CQ可得PQ=2HQ=8.
BC=3,在Rt△CHQ中,由勾股定理可得HQ=4,结合CP=CQ可得PQ=2HQ=8.
试题解析:
(![]() )∵
)∵![]() ,
, ![]() 均为等边三角形,
均为等边三角形,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
在![]() 和
和![]() 中,
中,
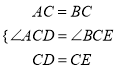 ,
,
∴![]() ≌
≌![]() .
.
(![]() )∵等边△ABC中,AO平分∠BAC,
)∵等边△ABC中,AO平分∠BAC,
∴∠CAD=![]() ∠BAC=30°.
∠BAC=30°.
如下图,过![]() 点作
点作![]() ,垂足为
,垂足为![]() ,
,
由(![]() )知
)知![]() ≌
≌![]() ,
,
则![]() ,
,
∴![]() ,
,
∴在![]() 中,
中, ![]() ,
,
又∵CP=CQ,CH⊥PQ,
∴![]() .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


