Question

【题目】点的坐标为，点的坐标为，点的坐标为．

（）在轴上是否存在点，使为等腰三角形，求出点坐标．

（）在轴上方存在点，使以点， ， 为顶点的三角形与全等，画出并请直接写出点的坐标．

Answer 1

【答案】（）， ， ， ;（）作图见解析,点的坐标为或．

【解析】试题分析：

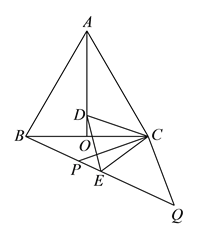
（1）如图1，分别以点B、C为圆心，BC为半径作圆交轴于点P1、P2、P3，作BC的垂直平分线交轴于点P4，这4个点为所求点，结合已知条件求出它们的坐标即可；

（2）如图2，根据成轴对称的两个三角形全等，作出点C关于直线AB的对称点D，连接BD、AD，所得△ABD为所求三角形；再作出点D关于直线的对称点D1，连接AD1、BD1，所得△ABD1也是所求三角形；即有两个符合要求的三角形；

试题解析：

（）如图1，∵点B、C的坐标分别为（0，2）、（1，0），

∴BC=.

分别以点B、C为圆心，BC为半径作圆交轴于点P1、P2、P3，

则OP1=OB+BP1=OB+BC=，OP2=BP2-OB=BC-OB=，OP3=OB=2；

设OP4= ，则BP4=CP4= ，在Rt△OCP4中，由勾股定理可得： ，解得： ，即OP4=；

∴①△P1BC是等腰三角形，BP1=BC，此时点P的坐标为；

②△P2BC是等腰三角形，BP2=BC，此时点P的坐标为；

③△P3BC是等腰三角形，P3C=BC，此时点P的坐标为；

④△P4BC是等腰三角形，BP4=CP4，此时点P的坐标为.

（）如图2，设点关于直线的对称点，则≌，

设过点， 的直线的解析式为．

则，

∴，

∴．

∴直线的解析式为．

由，

解得，

∴点．

∵，

∴，

根据对称性，点关于直线的对称点D1也满足条件．

综上所述，满足条件的点的坐标为或．