题目内容
 如图,已知:点A1、A2、A3、…在平面直角坐标系x轴上,点B1、B2、B3、…在直线
如图,已知:点A1、A2、A3、…在平面直角坐标系x轴上,点B1、B2、B3、…在直线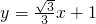 上,△OA1B1、△A1B2A2、△A2B3A3…均为等边三角形,求A2013的横坐标________.
上,△OA1B1、△A1B2A2、△A2B3A3…均为等边三角形,求A2013的横坐标________.
(22013-1)
分析:首先设直线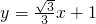 分别于x轴、y轴于点C、D,即可求得点C与D的坐标,即可求得∠OCD的度数,又由△OA1B1、△A1B2A2、△A2B3A3…均为等边三角形,易求得OB1=OC=
分别于x轴、y轴于点C、D,即可求得点C与D的坐标,即可求得∠OCD的度数,又由△OA1B1、△A1B2A2、△A2B3A3…均为等边三角形,易求得OB1=OC= ,A1B1=A1C,A2B2=A2C,则可得规律:OAn=(2n-1)
,A1B1=A1C,A2B2=A2C,则可得规律:OAn=(2n-1) .继而求得答案.
.继而求得答案.
解答: 解:设直线
解:设直线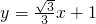 分别于x轴、y轴于点C、D,
分别于x轴、y轴于点C、D,
∴点C(- ,0),点D(0,1),
,0),点D(0,1),
∴OC= ,OD=1,
,OD=1,
∴tan∠OCD= =
= ,
,
∴∠OCD=30°,
∵△OA1B1、△A1B2A2、△A2B3A3…均为等边三角形,
∴∠A1OB1=∠A2A1B2=∠A3A2B3=60°,
∴∠OB1C=∠A1B2C=∠A2B3C=∠OCD=30°,
∴OB1=OC= ,A1B2=A1C,A2B3=A2C,
,A1B2=A1C,A2B3=A2C,
∴OA1=OB1= ,OA2=OA1+A1A2=OA1+A1B1=
,OA2=OA1+A1A2=OA1+A1B1= +2
+2 =3
=3 ,
,
同理:OA3=7 ,OA4=15
,OA4=15 ,
,
∴OAn=(2n-1) .
.
∴OA2013=(22013-1) .
.
故答案为:(22013-1) .
.
点评:此题考查了一次函数的性质、等边三角形的性质、等腰三角形的判定与性质以及三角函数的知识.此题难度较大,注意掌握数形结合思想的应用.

分析:首先设直线
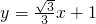 分别于x轴、y轴于点C、D,即可求得点C与D的坐标,即可求得∠OCD的度数,又由△OA1B1、△A1B2A2、△A2B3A3…均为等边三角形,易求得OB1=OC=
分别于x轴、y轴于点C、D,即可求得点C与D的坐标,即可求得∠OCD的度数,又由△OA1B1、△A1B2A2、△A2B3A3…均为等边三角形,易求得OB1=OC= ,A1B1=A1C,A2B2=A2C,则可得规律:OAn=(2n-1)
,A1B1=A1C,A2B2=A2C,则可得规律:OAn=(2n-1) .继而求得答案.
.继而求得答案.解答:
 解:设直线
解:设直线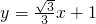 分别于x轴、y轴于点C、D,
分别于x轴、y轴于点C、D,∴点C(-
 ,0),点D(0,1),
,0),点D(0,1),∴OC=
 ,OD=1,
,OD=1,∴tan∠OCD=
 =
= ,
,∴∠OCD=30°,
∵△OA1B1、△A1B2A2、△A2B3A3…均为等边三角形,
∴∠A1OB1=∠A2A1B2=∠A3A2B3=60°,
∴∠OB1C=∠A1B2C=∠A2B3C=∠OCD=30°,
∴OB1=OC=
 ,A1B2=A1C,A2B3=A2C,
,A1B2=A1C,A2B3=A2C,∴OA1=OB1=
 ,OA2=OA1+A1A2=OA1+A1B1=
,OA2=OA1+A1A2=OA1+A1B1= +2
+2 =3
=3 ,
,同理:OA3=7
 ,OA4=15
,OA4=15 ,
,∴OAn=(2n-1)
 .
.∴OA2013=(22013-1)
 .
.故答案为:(22013-1)
 .
.点评:此题考查了一次函数的性质、等边三角形的性质、等腰三角形的判定与性质以及三角函数的知识.此题难度较大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 如图,已知等边△ABC中,DE∥BC,FG∥BC,现将等边△ABC分别沿DE和FG对折,点A分别落在点A1和点A2,连接A2B,A2C.
如图,已知等边△ABC中,DE∥BC,FG∥BC,现将等边△ABC分别沿DE和FG对折,点A分别落在点A1和点A2,连接A2B,A2C.
 如图,已知:点A1、A2、A3、…在平面直角坐标系x轴上,点B1、B2、B3、…在直线
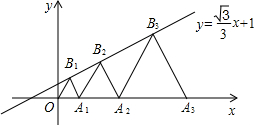
如图,已知:点A1、A2、A3、…在平面直角坐标系x轴上,点B1、B2、B3、…在直线 上,△OA1B1、△A1B2A2、△A2B3A3…均为等边三角形,求A2013 的横坐标 .
上,△OA1B1、△A1B2A2、△A2B3A3…均为等边三角形,求A2013 的横坐标 . 