题目内容
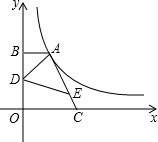 如图,点A在双曲线y=
如图,点A在双曲线y=| k |
| x |
| A、16 | ||
B、
| ||
C、
| ||
| D、9 |
考点:反比例函数综合题
专题:
分析:由AE=3EC,△ADE的面积为3,得到△CDE的面积为1,则△ADC的面积为4,设A点坐标为(a,b),则k=ab,AB=a,OC=2AB=2a,BD=OD=
b,利用S梯形OBAC=S△ABD+S△ADC+S△ODC得
(a+2a)×b=
a×
b+4+
×2a×
b,整理可得ab=
,即可得到k的值.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 16 |
| 3 |
解答: 解:连DC,如图,
解:连DC,如图,
∵AE=3EC,△ADE的面积为3,
∴△CDE的面积为1,
∴△ADC的面积为4,
设A点坐标为(a,b),则AB=a,OC=2AB=2a,
而点D为OB的中点,
∴BD=OD=
b,
∵S梯形OBAC=S△ABD+S△ADC+S△ODC,
∴
(a+2a)×b=
a×
b+4+
×2a×
b,
∴ab=
,
把A(a,b)代入双曲线y=
,
∴k=ab=
.
故选B.
 解:连DC,如图,
解:连DC,如图,∵AE=3EC,△ADE的面积为3,
∴△CDE的面积为1,
∴△ADC的面积为4,
设A点坐标为(a,b),则AB=a,OC=2AB=2a,
而点D为OB的中点,
∴BD=OD=
| 1 |
| 2 |
∵S梯形OBAC=S△ABD+S△ADC+S△ODC,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴ab=
| 16 |
| 3 |
把A(a,b)代入双曲线y=
| k |
| x |
∴k=ab=
| 16 |
| 3 |
故选B.
点评:本题考查了反比例函数综合题:点在反比例函数图象上,则点的横纵坐标满足其解析式;利用三角形的面积公式和梯形的面积公式建立等量关系.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 如图,若OA、OB是⊙O的半径,CB是⊙O的弦,∠AOB=64°,则∠ACB=( )
如图,若OA、OB是⊙O的半径,CB是⊙O的弦,∠AOB=64°,则∠ACB=( )| A、16° | B、58° |
| C、32° | D、64° |
 如图,长方形纸片ABCD中,AD=9,AB=3,将其折叠,使其点D与B重合,折痕为EF,则DE和EF长分别为( )
如图,长方形纸片ABCD中,AD=9,AB=3,将其折叠,使其点D与B重合,折痕为EF,则DE和EF长分别为( )A、4,
| ||
B、4,2
| ||
C、5,
| ||
D、5,2
|
二次函数y=-x2-6x+k的图象顶点在x轴上,则k的值为( )
| A、0 | B、-9 |
| C、9 | D、以上答案都不对 |
下列计算正确的是( )
A、2
| ||||||
B、
| ||||||
C、3
| ||||||
D、
|
 如图,矩形纸片ABCD中,AB=4,AD=8,折叠纸片使点D与点B重合,折痕为EF,则EF的长为( )
如图,矩形纸片ABCD中,AB=4,AD=8,折叠纸片使点D与点B重合,折痕为EF,则EF的长为( )| A、4.5 | ||
B、2
| ||
| C、5 | ||
| D、6 |
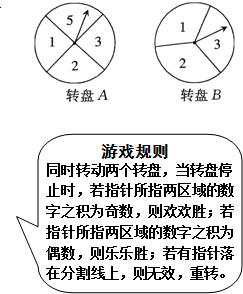 如图,把圆形转盘A平均4等份、圆形转盘B平均3等份,并在每一个小区域内标上数字.欢欢、乐乐两个人玩转盘戏,
如图,把圆形转盘A平均4等份、圆形转盘B平均3等份,并在每一个小区域内标上数字.欢欢、乐乐两个人玩转盘戏,