题目内容
 如图,矩形纸片ABCD中,AB=4,AD=8,折叠纸片使点D与点B重合,折痕为EF,则EF的长为( )
如图,矩形纸片ABCD中,AB=4,AD=8,折叠纸片使点D与点B重合,折痕为EF,则EF的长为( )| A、4.5 | ||
B、2
| ||
| C、5 | ||
| D、6 |
考点:翻折变换(折叠问题)
专题:
分析:本题可利用相似解决,由于折叠,可知BD⊥EF,利用直角三角形相似的性质:对应边成比例求得结果.
解答:
 解:如图,连结BD交EF于O.
解:如图,连结BD交EF于O.
∵折叠纸片使点D与点B重合,
∴BD⊥EF,BO=DO
∵四边形ABCD是矩形,
∴∠C=90°,BD=
=
=4
,BO=2
,
∵BD⊥EF,
∴∠BOF=∠C=90°,
又∵∠CBD=∠OBF,
∴△BOF∽△BCD,
∴
=
,即
=
,
∴OF=
,
∴EF=2
.
故选:B.

 解:如图,连结BD交EF于O.
解:如图,连结BD交EF于O.∵折叠纸片使点D与点B重合,
∴BD⊥EF,BO=DO
∵四边形ABCD是矩形,
∴∠C=90°,BD=
| BC2+CD2 |
| 82+42 |
| 5 |
| 5 |
∵BD⊥EF,
∴∠BOF=∠C=90°,
又∵∠CBD=∠OBF,
∴△BOF∽△BCD,
∴
| BO |
| BC |
| OF |
| CD |
2
| ||
| 8 |
| OF |
| 4 |
∴OF=
| 5 |
∴EF=2
| 5 |
故选:B.
点评:考查了翻折变换(折叠问题).折叠问题要要找清对应关系,重合的部分,重合的边,重合的角.这些关系在思考,做题时很有帮助.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
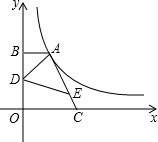 如图,点A在双曲线y=
如图,点A在双曲线y=| k |
| x |
| A、16 | ||
B、
| ||
C、
| ||
| D、9 |
若点A(-2,y1)、B(-1,y2)、C(1,y3)在反比例函数y=
的图象上,则( )
| -1 |
| x |
| A、y1>y2>y3 |
| B、y3>y2>y1 |
| C、y2>y1>y3 |
| D、y1>y3>y2 |
 如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得到折痕EC;将∠AEF对折,点A落在直线EF上的点A′处,得到折痕EN.
如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得到折痕EC;将∠AEF对折,点A落在直线EF上的点A′处,得到折痕EN.
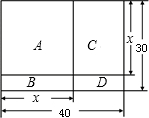 现有一块矩形场地,如图所示,长为40m,宽为30m,要将这块地划分为四块分别种植:A.兰花;B.菊花;C.月季;D.牵牛花.
现有一块矩形场地,如图所示,长为40m,宽为30m,要将这块地划分为四块分别种植:A.兰花;B.菊花;C.月季;D.牵牛花.