题目内容
【题目】杨辉是我国南宋时期杰出的数学家和教育家,下图是杨辉在公元1261年著作《详解九章算法》里面的一张图,即“杨辉三角”,该图中有很多规律,请仔细观察,解答下列问题: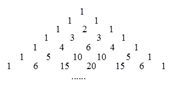
(1)图中给出了七行数字,根据构成规律,第8行中从左边数第3个数是;
(2)利用不完全归纳法探索出第n行中的所有数字之和为 .
【答案】
(1)21
(2)![]()
【解析】解:(1) 设第n行第2个数为 ![]() (n≥2,n为正整数),第n行第3个数为
(n≥2,n为正整数),第n行第3个数为 ![]() b(n≥3,n为正整数),观察,发现规律:
b(n≥3,n为正整数),观察,发现规律:
∵ ![]() =1,
=1, ![]() =2,
=2, ![]() =3,
=3, ![]() =4,
=4, ![]() =5,
=5,
∴ ![]() =n1;
=n1;
∵ ![]() =1,
=1, ![]() =3=1+2=
=3=1+2= ![]() +2,
+2, ![]() =6=3+3=
=6=3+3= ![]() +3,
+3, ![]() =10=6+4=
=10=6+4= ![]() +4,…,
+4,…,
∴ ![]()
![]() =n2,
=n2,
∴ ![]() =
= ![]() +
+ ![]()
![]() +
+ ![]()
![]() +
+ ![]() -
- ![]() +…+
+…+ ![]()
![]() =1+2+3+…+n2=
=1+2+3+…+n2= ![]() .
.
当n=8时, ![]() =
= ![]() =21.
=21.
⑵第一行数字之和1= ![]() ,第二行数字之和2=
,第二行数字之和2= ![]() ,第三行数字之和4=
,第三行数字之和4= ![]() ,第四行数字之和8=
,第四行数字之和8= ![]() ,…∴第n行数字之和为
,…∴第n行数字之和为 ![]() ,
,
本题主要考查数字的变化类,解题的关键是每行的数相加,分析总结得出规律,根据规律求出第n行的数据之和.

 阅读快车系列答案
阅读快车系列答案【题目】阅读理解:由面积都是1的小正方格组成的方格平面叫做格点平面.而纵横两组平行线的交点叫做格点.如图1中,有9个格点,如果一个正方形的每个顶点都在格点上,那么这个正方形称为格点正方形. 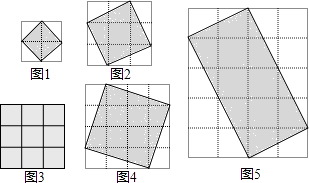
(1)探索发现:按照图形完成下表:
格点正方形边上格点数p | 格点正方形内格点数q |
| 格点正方形面积S | |
图1 | 4 | 1 | 2 | |
图2 | 4 | 4 | ||
图3 | 4 | 9 | ||
图4 | 4 |
关于格点正方形的面积S,从上述表格中你发现了什么规律?
(2)继续猜想:类比格点正方形的概念,如果一个长方形的每个顶点都在格点上,那么这个长方形称为格点长方形,对于格点长方形的面积,你认为也有类似(1)中的规律吗?试以图5中格点长方形为例来说明.