题目内容
若关于x的一元二次方程x2﹣2x+m=0有实数根,则m的取值范围是 .
m≤1 .
【考点】根的判别式.
【分析】方程有实数根即△≥0,根据△建立关于m的不等式,求m的取值范围.
【解答】解:由题意知,△=4﹣4m≥0,
∴m≤1
答:m的取值范围是m≤1.
【点评】总结:一元二次方程根的情况与判别式△的关系:
(1)△>0⇔方程有两个不相等的实数根;
(2)△=0⇔方程有两个相等的实数根;
(3)△<0⇔方程没有实数根.

练习册系列答案
相关题目
已知双曲线y=
 (k>0)与直线y=
(k>0)与直线y=
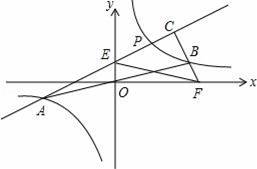
 x(k>0)交于A,B两点(点A在的B左侧)如图,点P是第一象限内双曲线上一动点,BC⊥AP于C,交x轴于F,PA交y轴于E,若AE2+BF2=m•EF2,则m= .
x(k>0)交于A,B两点(点A在的B左侧)如图,点P是第一象限内双曲线上一动点,BC⊥AP于C,交x轴于F,PA交y轴于E,若AE2+BF2=m•EF2,则m= .

九年级一班数学老师对全班学生在模拟考试中A卷成绩进行统计后,制成如下的统计表:
| 成绩(分) | 80 | 82 | 84 | 86 | 87 | 90 |
| 人数 | 8 | 12 | 9 | 3 | 5 | 8 |
则该班学生A卷成绩的众数和中位数分别是( )
A.82分,82分 B.82分,83分 C.80分,82分 D.82分,84分

 ,再求当a=
,再求当a=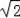
 ﹣1时代数式的值.
﹣1时代数式的值.

 D.
D.