题目内容
 已知△ABC内接于⊙O,CE是⊙O的直径,高CD⊥AB,垂足为D,
已知△ABC内接于⊙O,CE是⊙O的直径,高CD⊥AB,垂足为D,
(1)求证:△CAE∽△CDB;
(2)若AC=3,CB=1,CD=0.75,求CE的长.
(1)证明:
∵CE是⊙O的直径,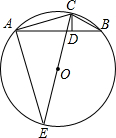
∴∠CAE=90°,∠AEC=∠ABC,
∵CD⊥AB,
∴∠CAE=∠BDC=90°
∴△CAE∽△CDB;
(2)∵CB=1,CD=0.75,AC=3,
∴DB=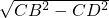 =
= ,
,
∵△CAE∽△CDB,
∴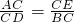 ,
,
∴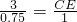 ,
,
∴CE=4.
分析:(1)由两对角相等的三角形相似即可证明:△CAE∽△CDB;
(2)利用相似三角形的性质可即可求出CE的长.
点评:本题考查了圆周角定理的运用、相似三角形的判定和性质,题目比较简单.
∵CE是⊙O的直径,

∴∠CAE=90°,∠AEC=∠ABC,
∵CD⊥AB,
∴∠CAE=∠BDC=90°
∴△CAE∽△CDB;
(2)∵CB=1,CD=0.75,AC=3,
∴DB=
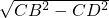 =
= ,
,∵△CAE∽△CDB,
∴
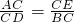 ,
,∴
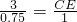 ,
,∴CE=4.
分析:(1)由两对角相等的三角形相似即可证明:△CAE∽△CDB;
(2)利用相似三角形的性质可即可求出CE的长.
点评:本题考查了圆周角定理的运用、相似三角形的判定和性质,题目比较简单.

练习册系列答案
相关题目
 如图,已知△ABC内接于⊙O,D是⊙O上一点,连接BD、CD、AC、BD交于点E.
如图,已知△ABC内接于⊙O,D是⊙O上一点,连接BD、CD、AC、BD交于点E.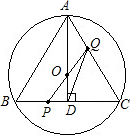 终点C运动,速度为1cm/s;点Q沿CA向终点A运动,速度为2cm/s,设它们运动的时间为x(s).
终点C运动,速度为1cm/s;点Q沿CA向终点A运动,速度为2cm/s,设它们运动的时间为x(s).
 (2013•樊城区模拟)如图,已知△ABC内接于⊙O,弦AD交BC于E,过点D的切线MN交直线AB于M,交直线AC于N.
(2013•樊城区模拟)如图,已知△ABC内接于⊙O,弦AD交BC于E,过点D的切线MN交直线AB于M,交直线AC于N. (2013•永州)如图,已知△ABC内接于⊙O,BC是⊙O的直径,MN与⊙O相切,切点为A,若∠MAB=30°,则∠B=
(2013•永州)如图,已知△ABC内接于⊙O,BC是⊙O的直径,MN与⊙O相切,切点为A,若∠MAB=30°,则∠B=