Question

如图，直角梯形OABC中，AB∥OC，O为坐标原点，点A在y轴正半轴上，点C在x轴正半轴上，点B坐标为(2，2)，∠BCO＝60°，OH⊥BC于点H．动点P从点H出发，沿线段HO向点O运动，动点Q从点O出发，沿线段OA向点A运动，两点同时出发，速度都为每秒1个单位长度．设点P运动的时间为t秒．

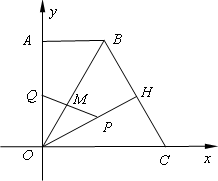
(1)求OH的长；

(2)若△OPQ的面积为S(平方单位)．求S与t之间的函数关系式．并求t为何值时，△OPQ的面积最大，最大值是多少？

(3)设PQ与OB交于点M．①当△OPM为等腰三角形时，求(2)中S的值．

②探究线段OM长度的最大值是多少，直接写出结论．

Answer 1

答案：
解析：

解：(1)∵∥ 　　∴ 　　在中，， 　　∴， 　　∴　而 　　∴为等边三角形 　　∴　　(3分) 　　(2)∵ 　　∴　 　　∴ 　　＝()　　(6分) 　　即 　　∴当时，　　(7分) 　　(3)①若为等腰三角形，则： 　　(i)若， 　　∴∥ 　　∴即 　　解得： 　　此时　　(8分) 　　(ii)若， 　　∴ 　　过点作，垂足为，则有： 　　 　　即 　　解得： 　　此时　　(9分) 　　(iii)若， 　　∴∥ 　　此时在上，不满足题意　　(10分) 　　②线段长的最大值为　　(12分)