题目内容
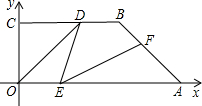
 如图,直角梯形OABF中,∠OAB=∠B=90°,A点在x轴上,双曲线y=
如图,直角梯形OABF中,∠OAB=∠B=90°,A点在x轴上,双曲线y=| k |
| x |
| BF |
| OA |
| 2 |
| 3 |
分析:由于BF:OA=2:3,可以设F(m,n)则OA=3m,BF=2m,由于S△BEF=4,则BE=
,然后即可求出E(3m,n-
),
依据mn=3m(n-
)可求mn=6,即求出了k.
| 4 |
| m |
| 4 |
| m |
依据mn=3m(n-
| 4 |
| m |
解答: 解:如图,过F作FC⊥OA于C,
解:如图,过F作FC⊥OA于C,
∵BF:OA=2:3
∴OA=3OC,BF=2OC
∴若设F(m,n)
则OA=3m,BF=2m
∵S△BEF=4
∴BE=
则E(3m,n-
)
∵E在双曲线y=
上
∴mn=3m(n-
)
∴mn=6
即k=6.
故答案为:6.
 解:如图,过F作FC⊥OA于C,
解:如图,过F作FC⊥OA于C,∵BF:OA=2:3
∴OA=3OC,BF=2OC
∴若设F(m,n)
则OA=3m,BF=2m
∵S△BEF=4
∴BE=
| 4 |
| m |
则E(3m,n-
| 4 |
| m |
∵E在双曲线y=
| k |
| x |
∴mn=3m(n-
| 4 |
| m |
∴mn=6
即k=6.
故答案为:6.
点评:此题难度较大,主要考查反比例函数的图象和性质、用坐标表示线段长和三角形面积,综合性比较强.

练习册系列答案
相关题目

 如图,直角梯形OABC中,∠OAB=∠B=90°,A点在x轴上,双曲线y=
如图,直角梯形OABC中,∠OAB=∠B=90°,A点在x轴上,双曲线y=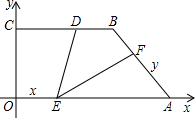 是BC上一点,BD=
是BC上一点,BD=