��Ŀ����
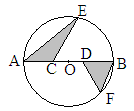
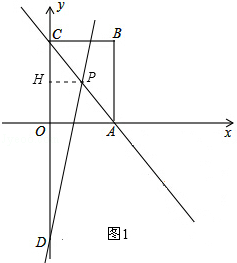
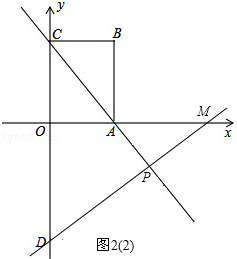
��֪��ͼƽ��ֱ������ϵ�У���O������ԭ�㣬����ABCD�Ƕ�������ֱ�ΪA��3��0����B��3��4����C��0��4������D��y���ϣ��ҵ�D������Ϊ��0����5������P��ֱ��AC�ϵ�һ���㣮
��1������P�˶����߶�AC���е�ʱ����ֱ��DP�Ľ���ʽ����ϵʽ����
��2������P��ֱ��AC�ƶ�ʱ������D��P��ֱ����x�ύ�ڵ�M������x������������Ƿ����ʹ��DOM���ABC���Ƶĵ�M�������ڣ��������M�����ꣻ�������ڣ���˵�����ɣ�
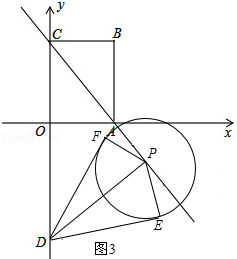
��3������P��ֱ��AC�ƶ�ʱ���Ե�PΪԲ�ġ�R��R��0��Ϊ�뾶����Բ���õ���Բ��Ϊ��ԲP�����趯ԲP�İ뾶��Ϊ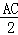 ������D����ԲP�����������붯ԲP�ֱ������ڵ�E��F����̽���ڶ�ԲP���Ƿ���������С���ı���DEPF�������ڣ��������С���S��ֵ���������ڣ���˵�����ɣ�
������D����ԲP�����������붯ԲP�ֱ������ڵ�E��F����̽���ڶ�ԲP���Ƿ���������С���ı���DEPF�������ڣ��������С���S��ֵ���������ڣ���˵�����ɣ�
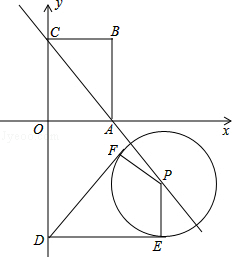
��1������P�˶����߶�AC���е�ʱ����ֱ��DP�Ľ���ʽ����ϵʽ����
��2������P��ֱ��AC�ƶ�ʱ������D��P��ֱ����x�ύ�ڵ�M������x������������Ƿ����ʹ��DOM���ABC���Ƶĵ�M�������ڣ��������M�����ꣻ�������ڣ���˵�����ɣ�
��3������P��ֱ��AC�ƶ�ʱ���Ե�PΪԲ�ġ�R��R��0��Ϊ�뾶����Բ���õ���Բ��Ϊ��ԲP�����趯ԲP�İ뾶��Ϊ
 ������D����ԲP�����������붯ԲP�ֱ������ڵ�E��F����̽���ڶ�ԲP���Ƿ���������С���ı���DEPF�������ڣ��������С���S��ֵ���������ڣ���˵�����ɣ�
������D����ԲP�����������붯ԲP�ֱ������ڵ�E��F����̽���ڶ�ԲP���Ƿ���������С���ı���DEPF�������ڣ��������С���S��ֵ���������ڣ���˵�����ɣ�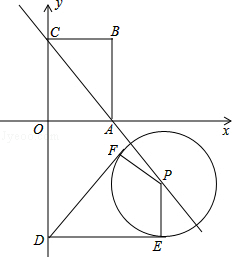
��1��y=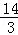 x��5
x��5
��2��M��������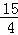 ��0����
��0����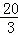 ��0��
��0��
��3�����ڣ�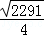
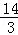 x��5
x��5��2��M��������
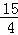 ��0����
��0����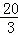 ��0��
��0����3�����ڣ�
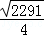
�����������1��ֻ�������AC�е�P�����꣬Ȼ���ô���ϵ�����������ֱ��DP�Ľ���ʽ��
��2�����ڡ�DOM���ABC���ƣ���Ӧ��ϵ��ȷ�����ɷ���������������ۣ������������������OM�ij������������M�����꣮
��3����֤S��PED=S��PFD���Ӷ���S�ı���DEPF=2S��PED=
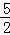 DE���ɡ�DEP=90���DE2=DP2��PE2=DP2��
DE���ɡ�DEP=90���DE2=DP2��PE2=DP2��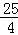 �����ݡ��㵽ֱ��֮�䣬���߶���̡��ɵã���DP��ACʱ��DP��̣���ʱDEҲ��̣���Ӧ���ı���DEPF�������С�����������������ƣ��������DP��ACʱDP��ֵ���Ϳ�����ı���DEPF�������Сֵ��
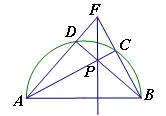
�����ݡ��㵽ֱ��֮�䣬���߶���̡��ɵã���DP��ACʱ��DP��̣���ʱDEҲ��̣���Ӧ���ı���DEPF�������С�����������������ƣ��������DP��ACʱDP��ֵ���Ϳ�����ı���DEPF�������Сֵ���⣺��1������P��PH��OA����OC�ڵ�H����ͼ1��ʾ��
��PH��OA��
���CHP�ס�COA��
��
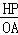 =
=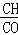 =
=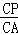 ��
���ߵ�P��AC�е㣬
��CP=
 CA��
CA����HP=
 OA��CH=
OA��CH= CO��
CO����A��3��0����C��0��4����
��OA=3��OC=4��
��HP=
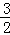 ��CH=2��
��CH=2����OH=2��
��PH��OA����COA=90�㣬
���CHP=��COA=90�㣮
���P��������
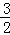 ��2����
��2������ֱ��DP�Ľ���ʽΪy=kx+b��
��D��0����5����P��
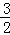 ��2����ֱ��DP�ϣ�
��2����ֱ��DP�ϣ���
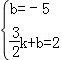
��
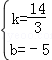
��ֱ��DP�Ľ���ʽΪy=
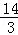 x��5��
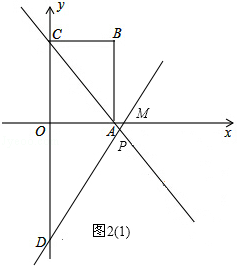
x��5����2��������DOM�ס�ABC��ͼ2��1����ʾ��
�ߡ�DOM�ס�ABC��
��
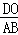 =
=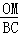 ��
���ߵ�B����Ϊ��3��4������D������Ϊ��0����5����
��BC=3��AB=4��OD=5��
��
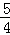 =
=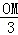 ��
����OM=
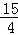 ��
���ߵ�M��x����������ϣ�
���M��������
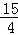 ��0��
��0��������DOM�ס�CBA����ͼ2��2����ʾ��
�ߡ�DOM�ס�CBA��
��
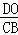 =
=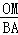 ��
����BC=3��AB=4��OD=5��
��
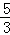 =
=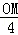 ��
����OM=
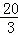 ��
���ߵ�M��x����������ϣ�
���M��������
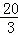 ��0����
��0������������������DOM���CBA���ƣ����M������Ϊ��
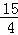 ��0����
��0����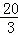 ��0����
��0������3����OA=3��OC=4����AOC=90�㣬
��AC=5��
��PE=PF=
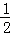 AC=
AC=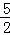 ��
����DE��DF�����P����
��DE=DF����DEP=��DFP=90�㣮
��S��PED=S��PFD��
��S�ı���DEPF=2S��PED=2��
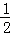 PE•DE=PE•DE=
PE•DE=PE•DE=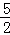 DE��
DE���ߡ�DEP=90�㣬
��DE2=DP2��PE2��=DP2��
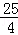 ��
�����ݡ��㵽ֱ��֮�䣬���߶���̡��ɵã�
��DP��ACʱ��DP��̣�
��ʱDEȡ����Сֵ���ı���DEPF�������С��
��DP��AC��
���DPC=90�㣮
���AOC=��DPC��
�ߡ�OCA=��PCD����AOC=��DPC��
���AOC�ס�DPC��
��
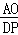 =
=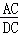 ��
����AO=3��AC=5��DC=4������5��=9��
��
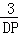 =
=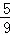 ��
����DP=
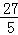 ��
����DE2=DP2��
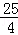 =��
=��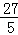 ��2��
��2��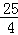 =
=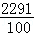 ��
����DE=
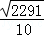 ��
����S�ı���DEPF=
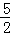 DE=
DE=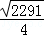 ��
�����ı���DEPF�������СֵΪ
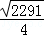 ��
��

��ϰ��ϵ�д�
 ��У������Ԫͬ��ѵ��������ϵ�д�
��У������Ԫͬ��ѵ��������ϵ�д�
�����Ŀ
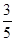 ��OA=10cm����AB��Ϊ cm��
��OA=10cm����AB��Ϊ cm��