Question

如图，在方格纸中，直线m与n相交于点C，
（1）请过点A画直线AB，使AB⊥m，垂足为点B；
（2）请过点A画直线AD，使AD∥m；交直线n于点D；
（3）若方格纸中每个小正方形的边长为1，求四边形ABCD的面积。

Answer 1

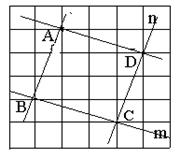四边形ABCD的面积为10

解析试题分析：根据题意借助三角板做m的垂线后，因为AD∥m，所以AD⊥AB。可做出AD线。得图像。可知这四条线围成的长方形由中心的4个小正方形和4个全等的直角三角形围成。这4个全等三角形刚好可以拼成由6个小正方形构成的长方形。故四边形ABCD共占了10个小正方形。所以：四边形ABCD的面积为10。
考点：直线的位置关系与几何面积
点评：本题难度中等。做这类无法直接求面积的题时候，注意要能够转化为其他图形的面积来计算。