题目内容
5. 已知:如图,AD是△ABC的高,BE⊥AB,AE交BC于点F,AB•AC=AD•AE.求证:△BEF∽△ACF.
已知:如图,AD是△ABC的高,BE⊥AB,AE交BC于点F,AB•AC=AD•AE.求证:△BEF∽△ACF.
分析 先证明△ABE∽△ADC,得出对应角相等∠DAC=∠BAE,证出∠E=∠C,由对顶角相等∠BFE=∠AFC,即可得出△BEF∽△ACF.
解答 证明:∵AD是△ABC的高,
∴∠ADC=9O°,
∵BE⊥AB,
∴∠EBA=90°,
∴∠ADC=∠EBA,
∵AB•AC=AD•AE,
∴$\frac{AB}{AD}=\frac{AE}{AC}$,
∴△ABE∽△ADC,
∴∠DAC=∠BAE,
∵∠E+∠BAE=90°,∠C+∠DAC=90°,
∴∠E=∠C,
∵∠BFE=∠AFC,
∴△BEF∽△ACF.
点评 本题考查了相似三角形的判定与性质;熟练掌握相似三角形的判定方法,证明三角形相似得出对应角相等是解决问题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
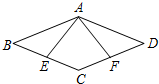 如图,在菱形ABCD中,E、F分别是BC,CD的中点,且AE⊥BC,AF⊥CD.求菱形各个内角的度数.
如图,在菱形ABCD中,E、F分别是BC,CD的中点,且AE⊥BC,AF⊥CD.求菱形各个内角的度数.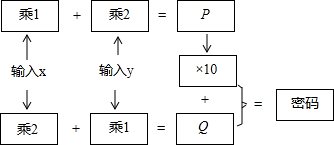 如图是一个密码产生程序,输入数字x、y(1~9)后进行若干步计算分别得到P和Q,再由10P+Q的值确定一个密码,如果要产生密码96,那么x=1,y=4.
如图是一个密码产生程序,输入数字x、y(1~9)后进行若干步计算分别得到P和Q,再由10P+Q的值确定一个密码,如果要产生密码96,那么x=1,y=4.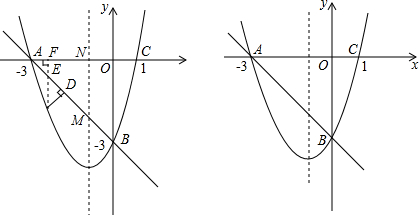
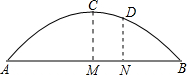 如图,一石拱桥呈抛物线状,已知石拱跨度AB为40米,拱高CM为16米,把桥拱看作一个二次函数的图象,建立适当的坐标系.
如图,一石拱桥呈抛物线状,已知石拱跨度AB为40米,拱高CM为16米,把桥拱看作一个二次函数的图象,建立适当的坐标系.