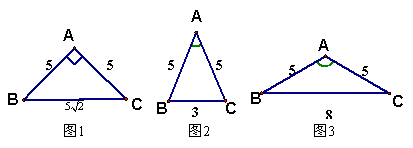题目内容

D是等腰锐角三角形ABC的底边BC上一点，则AD，BD，CD满足关系式（　　）

A、AD²=BD²+CD²

B、AD²＞BD²+CD²

C、2AD²=BD²+CD²

D、2AD²＞BD²+CD²

分析：以等边三角形为例，
当D为BC边上的中点时，有AD²＞BD²+CD²；
当D为BC边的端点时，有AD²=2（BD²+CD²），
故有2AD²＞BD²+CD²．

解答：解：在等边三角形ABC中，

当AD⊥BC时，则AD为等边三角形的中线，即D为中点，
有AD²＞BD²+CD²；
当D为BC边的端点时，有AD²=2（BD²+CD²），
根据极限求值法，可知2AD²＞BD²+CD²．
故选D．

点评：本题考查极限求值法的运用，而且取D为BC的中点和D为BC边端点的两个极限值，运用勾股定理求解．

练习册系列答案

国华考试中考总动员系列答案

D是等腰锐角三角形ABC的底边BC上的一点，则AD，BD，CD满足关系式

小红学完“等腰三角形”和“勾股定理”后，进行了如下的探究：

等腰△ABC中，AB=AC，当AB²+AC²=BC²时，可得∠A=90°，即△ABC是等腰直角三角形（如图1）猜想：

【1】当AB²+AC²>BC²时，可得∠A<90°，即△ABC是等腰锐角三角形（如图2）；

【2】当AB²+AC²<BC²时，可得________，即___________________( 如图3)

小红总结出：可以从等腰三角形三边的数量关系，进一步明确三角形的形状.

应用：（1）在图2的条件下（即AB=AC=5，BC=3），在边BC上是否存在点M，使MA与三角形的一腰垂直？请选择_______ A. 存在　　 B.不存在

　（2）在图3的条件下（即AB=AC=5，BC=8），在边BC上是否存在点M，使得MA与三角形的一边垂直，若存在，请你求出满足条件时BM的长度；若不存在，请说明理由.

D是等腰锐角三角形ABC的底边BC上一点，则AD，BD，CD满足关系式( )

A.AD²=BD²+CD². B．AD²＞BD²+CD². C．2AD²=BD²+CD². D．2AD²＞BD²+CD²

试题分类