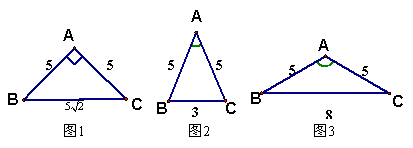题目内容
D是等腰锐角三角形ABC的底边BC上的一点,则AD,BD,CD满足关系式
- A.AD2=BD2+CD2.
- B.AD2>BD2+CD2.
- C.2AD2=BD2+CD2.
- D.2AD2>BD2+CD2.
D
以等边三角形为例,当D为BC边上的中点时,有AD2>BD2+CD2,当D为BC边的端点时,有AD2=BD2+CD2,故有2AD2>BD2+CD2.故选D.
以等边三角形为例,当D为BC边上的中点时,有AD2>BD2+CD2,当D为BC边的端点时,有AD2=BD2+CD2,故有2AD2>BD2+CD2.故选D.

练习册系列答案
相关题目