题目内容
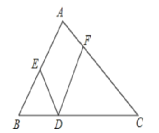
【题目】如图所示,在△ABC中,点D. E. F分别在BC、AB、AC上,且BD=BE,CD=CF,∠EDF=50°.则∠A的度数为___________.
【答案】80°
【解析】
由∠EDF=50°可得∠BDE+∠CDF=130°,根据三角形内角和定理可求出∠B+∠C,就可求出∠A.
∵BD=BE,CD=CF,
∴∠BDE=∠BED,∠CDF=∠CFD.
∵∠BDE+∠EDF+∠CDF=180°,∠EDF=50°,
∴∠BDE+∠CDF=130°.
∵∠B+∠BDE+∠BED=180°,∠C+∠CDF+∠CFD=180°,
∴∠B+∠BDE+∠BED+∠C+∠CDF+∠CFD=360°.
∴∠B+∠C+2∠BDE+2∠CDF=360°.
∴∠B+∠C+260°=360°.
∴∠B+∠C=100°.
∵∠A+∠B+∠C=180°,
∴∠A=80°.
故答案为:80°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
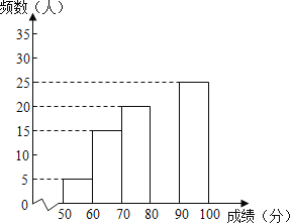
【题目】某学校七年级举行“每天锻炼一小时,健康生活一辈子”为主题的一分钟跳绳大赛,校团委组织了全级1000名学生参加为了解本次大赛的成绩,校团委随机抽取了其中100名学生的成绩作为样本进行统计,制成如下不完整的统计图表根据所给信息,解答下列问题;
(1)m=______,n=______.
(2)补全频数分布直方图;
(3)若成绩在80分以上(包括80分)为“优”,请你估计该校七年级参加本次比赛的1000名学生中成绩是“优”的有多少人.
成绩x(分) | 频数(人) | 频率 |
50≤x<60 | 5 | 5% |
60≤x<70 | 15 | 15% |
70≤x<80 | 20 | 20% |
80≤x<90 | m | 35% |
90≤x≤100 | 25 | n |