Question

17．如图所示，小路是由黑色的正方形理石和白色的三角形理石铺成，已知中间所有正方形的面积之和是m平方米，小路的左侧的所有三角形面积之和为n平方米，则这条小路一共占地的面积是2n+m平方米．（直接写出答案即可）．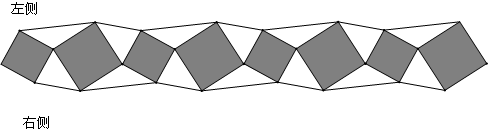

Answer 1

分析 根据题意结合全等三角形的判定与性质，可得左侧与右侧相对应的三角形的面积相等，然后列式计算即可得解．

解答 解：过点A作AB⊥CB垂足为B，过点D作DE⊥CE，垂足为E，
∵∠ACB+∠BCD=∠BCD+∠ECD=90°，
∴∠ACB=∠ECD，
在△ACB和△DCE中，
∵$\left\{\begin{array}{l}{∠ABC=∠DEC}\\{∠BCA=∠ECD}\\{AC=DC}\end{array}\right.$，
∴△ACB≌△DCE（AAS），
∴AB=DE，
∴上下两三角形面积相等，
∵小路的左侧的所有三角形面积之和为n平方米，
∴小路的右侧的所有三角形面积之和为n平方米，
∴这条小路一共占地的面积是：2n+m平方米．
故答案为：2n+m．

点评 此题主要考查了全等三角形的应用，得出左侧与右侧相对应的三角形的面积相等是解题关键．