题目内容
如图,点E、F、G、H分别在菱形ABCD的四条边上,且BE=BF=DG=DH,连接EF,FG,GH,HE得到四边形EFGH.
(1)求证:四边形EFGH是矩形;
(2)设AB=a,∠A=60°,当BE为何值时,矩形EFGH的面积最大?

【考点】菱形的性质;二次函数的最值;矩形的判定与性质.
【分析】(1)利用等腰三角形的性质:等边对等角,以及平行线的性质可以证得∠DGH+∠CGH=90°,则∠HGF=90°,根据三个角是直角的四边形是矩形,即可证得;
(2)设BE的长是x,则利用x表示出矩形EFGH的面积,根据函数的性质即可求解.
【解答】(1)证明:∵DG=DH,
∴∠DHG=∠DGH=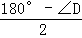 ,
,
同理,∠CGF=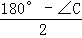 ,
,
∴∠DGH+∠CGF=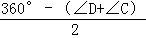 ,
,
又∵菱形ABCD中,AD∥BC,
∴∠D+∠C=180°,
∴∠DGH+∠CGF=90°,
∴∠HGF=90°,
同理,∠GHE=90°,∠EFG=90°,
∴四边形EFGH是矩形;
(2)AB=a,∠A=60°,则菱形ABCD的面积是: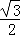 a2,
a2,
设BE=x,则AE=a﹣x,
则△AEH的面积是: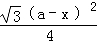 ,
,
△BEF的面积是: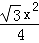 ,
,
则矩形EFGH的面积y=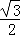 a2﹣
a2﹣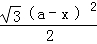 ﹣
﹣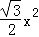 ,
,
即y=﹣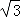 x2+
x2+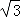 ax,
ax,
则当x=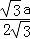 =
=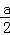 时,函数有最大值.
时,函数有最大值.
此时BE=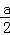 .
.
【点评】本题考查了菱形的性质,矩形的判定以及二次函数的性质,正确利用x表示出矩形EFGH的面积是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目