题目内容
15. 如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )
如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )| A. | 2$\sqrt{2}$<r<$\sqrt{17}$ | B. | $\sqrt{17}$<r≤3$\sqrt{2}$ | C. | $\sqrt{17}$<r<5 | D. | 5<r<$\sqrt{29}$ |
分析 利用勾股定理求出各格点到点A的距离,结合点与圆的位置关系,即可得出结论.
解答 解:给各点标上字母,如图所示.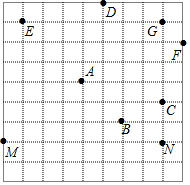
AB=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,AC=AD=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$,AE=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,AF=$\sqrt{{5}^{2}+{2}^{2}}$=$\sqrt{29}$,AG=AM=AN=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴$\sqrt{17}$<r≤3$\sqrt{2}$时,以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内.
故选B.
点评 本题考查了点与圆的位置关系以及勾股定理,利用勾股定理求出各格点到点A的距离是解题的关键.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
6.不等式5x>4x+2的解集在数轴上表示正确的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
20. 如图,点C是以AB为直径的半圆O的三等分点,AC=2,则图中阴影部分的面积是( )
如图,点C是以AB为直径的半圆O的三等分点,AC=2,则图中阴影部分的面积是( )
 如图,点C是以AB为直径的半圆O的三等分点,AC=2,则图中阴影部分的面积是( )
如图,点C是以AB为直径的半圆O的三等分点,AC=2,则图中阴影部分的面积是( )| A. | $\frac{4π}{3}$$-\sqrt{3}$ | B. | $\frac{4π}{3}$-2$\sqrt{3}$ | C. | $\frac{2π}{3}$$-\sqrt{3}$ | D. | $\frac{2π}{3}$-$\frac{\sqrt{3}}{2}$ |
7.下列各组数中,把两数相乘,积为1的是( )
| A. | 2和-2 | B. | -2和$\frac{1}{2}$ | C. | $\sqrt{3}$和$\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$和-$\sqrt{3}$ |
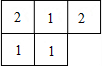 由7个相同的小正方体搭成一个几何体,其俯视图如图所示,其中小正方形中数字表示该位置小正方体的个数,则该几何体的左视图是( )
由7个相同的小正方体搭成一个几何体,其俯视图如图所示,其中小正方形中数字表示该位置小正方体的个数,则该几何体的左视图是( )


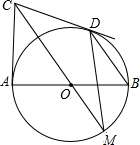 如图.AB为⊙O的直径.CA,CD分别切⊙O于A、D,CO的延长线交⊙O于M,连BD、DM.
如图.AB为⊙O的直径.CA,CD分别切⊙O于A、D,CO的延长线交⊙O于M,连BD、DM. 如图,在直角坐标系中,⊙A的圆心A的坐标为(-1,0),半径为1,点P为直线y=-$\frac{3}{4}$x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是2$\sqrt{2}$.
如图,在直角坐标系中,⊙A的圆心A的坐标为(-1,0),半径为1,点P为直线y=-$\frac{3}{4}$x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是2$\sqrt{2}$. 海轮以每小时30nmile的速度航行,在点A处测得海上油井P在它的南偏东60°方向,向北航行40min后到达B处,测得油井P在南偏东30°方向,海轮改北偏东60在再航行120min到达C处,求P,C间的距离及此时点C在油井P的什么方向.
海轮以每小时30nmile的速度航行,在点A处测得海上油井P在它的南偏东60°方向,向北航行40min后到达B处,测得油井P在南偏东30°方向,海轮改北偏东60在再航行120min到达C处,求P,C间的距离及此时点C在油井P的什么方向.