题目内容
已知x、y是非负实数,x+2y-8=0,则xy的最大值是
8
8
.分析:首先在二元一次方程组中用x表示y,然后得到有关x的二次函数确定最大值即可;
解答:解:∵x、y是非负实数,x+2y-8=0,
∴y=-
x+4
∴xy=-
(x2-8x+16-16)=-
(x-4)2+8
∴xy的最大值为8,
故答案为:8
∴y=-
| 1 |
| 2 |
∴xy=-
| 1 |
| 2 |
| 1 |
| 2 |
∴xy的最大值为8,
故答案为:8
点评:本题主要考查了求函数最值,同时考查了运算求解的能力,属于基础题.

练习册系列答案
相关题目
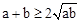 .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.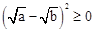 ,∴
,∴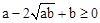 .
.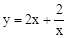 的最小值.
的最小值.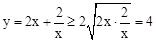 .当且仅当
.当且仅当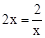 ,即x=1时,“=”成立.
,即x=1时,“=”成立.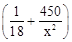 升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.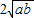 .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.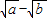 )2≥0,∴a-
)2≥0,∴a-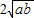 +b≥0.
+b≥0.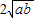 .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.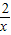 的最小值.
的最小值.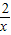 ≥
≥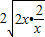 =4.当且仅当2x=
=4.当且仅当2x=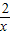 ,即x=1时,“=”成立.
,即x=1时,“=”成立.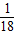 +
+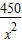 )升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
)升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.