题目内容
14. 如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕.
如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕.(1)试判断B′E与DC的位置关系,并说明理由;
(2)如果∠C=128°,求∠AEB的度数.
分析 (1)由折叠得:∠AB′E=∠B=∠D=90°,再根据同位角相等两直线平行可得B′E∥CD;
(2)根据平行线的性质求得∠B′EB,由折叠的性质得∠AEB=∠AEB′,即可求得结论.
解答 (1)B′E∥DC,
证明:由折叠得:∠AB′E=∠B=∠D=90°,
∴B′E∥DC;
(2)解:∵B′E∥DC,∠C=128°,
∴∠B′EB=128°,
由折叠得:∠AEB=∠AEB′=$\frac{1}{2}$×128°=64°.
点评 本题主要考查了平行线的性质和判定,知道翻折变换前后的两个图形全等是解题的关键.

练习册系列答案
相关题目
4.下列各式是分式的是( )
| A. | $\frac{x}{2}$ | B. | $\frac{x}{π}$ | C. | $\frac{2}{x}$ | D. | $\frac{x+y}{2}$ |
9.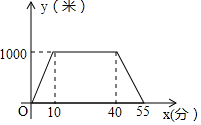 小明从家里出发到超市进行购物后返回,小明离开家的路程y(米)与所用时间x(分)之间的关系如图,则下列说法不正确的是( )
小明从家里出发到超市进行购物后返回,小明离开家的路程y(米)与所用时间x(分)之间的关系如图,则下列说法不正确的是( )
 小明从家里出发到超市进行购物后返回,小明离开家的路程y(米)与所用时间x(分)之间的关系如图,则下列说法不正确的是( )
小明从家里出发到超市进行购物后返回,小明离开家的路程y(米)与所用时间x(分)之间的关系如图,则下列说法不正确的是( )| A. | 小明家到超市的距离是1000米 | B. | 小明在超市购物的时间为30分钟 | ||
| C. | 小明离开家的时间共55分钟 | D. | 小明返回的速度比去时的速度快 |
19. 如图,将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为( )
如图,将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为( )
 如图,将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为( )
如图,将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为( )| A. | 11 | B. | 10 | C. | 9 | D. | 8 |
6.分式方程$\frac{1}{x-2}$=$\frac{3}{x}$的解是( )
| A. | x=-2 | B. | x=-3 | C. | x=2 | D. | x=3 |
3.下列图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4.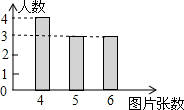 若干名同学制作卡通图片,他们制作的卡通图片张数的条形统计图如图所示,设他们制作的卡通图片的张数的平均数为a,中位数为b,众数为c,则a,b,c的大小关系为( )
若干名同学制作卡通图片,他们制作的卡通图片张数的条形统计图如图所示,设他们制作的卡通图片的张数的平均数为a,中位数为b,众数为c,则a,b,c的大小关系为( )
 若干名同学制作卡通图片,他们制作的卡通图片张数的条形统计图如图所示,设他们制作的卡通图片的张数的平均数为a,中位数为b,众数为c,则a,b,c的大小关系为( )
若干名同学制作卡通图片,他们制作的卡通图片张数的条形统计图如图所示,设他们制作的卡通图片的张数的平均数为a,中位数为b,众数为c,则a,b,c的大小关系为( )| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | c>a>b |
 如图,在△ABC中,AB=AC,BD和CE是△ABC的中线,∠ABD=30°,∠BCE=40°,则∠ABC的度数为70°.
如图,在△ABC中,AB=AC,BD和CE是△ABC的中线,∠ABD=30°,∠BCE=40°,则∠ABC的度数为70°.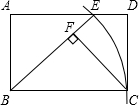 如图,在矩形ABCD中,以点B为圆心、BC长为半径圆弧,交AD边于点E,连接BE,过点C作CF⊥BE,垂足为F.
如图,在矩形ABCD中,以点B为圆心、BC长为半径圆弧,交AD边于点E,连接BE,过点C作CF⊥BE,垂足为F.