题目内容
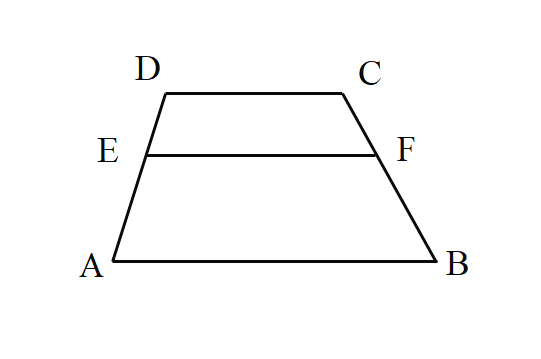
【题目】如图，已知在梯形ABCD中，AB//CD，AB=12，CD=7，点E在边AD上，
，过点E作EF//AB交边BC于点F.
（1）求线段EF的长；
（2）设
，
，联结AF，请用向量
表示向量
.
【答案】（1）9；（2）
【解析】
(1)过D作BC的平行线分别交EF于M，AB于G，由DE：AE=2：3，即可求得
，然后在梯形ABCD中，AB∥CD，AB=12，CD=7，根据平行线分线段成比例定理，即可求得EF的长．
(2)根据（1）中的比例关系写出向量即可.
解：(1) 过D作BC的平行线分别交EF于M，AB于G，
∵
,∴.
又∵EF∥AB，AB∥CD，AB=12，CD=7，
∴CD=MF=GB=7，
∴AG=5.
∴EM=
AG=2.
∴EF=EM+MF=9．
(2)∵ 
，
，由（1）知，
练习册系列答案
阅读快车系列答案
相关题目
