Question

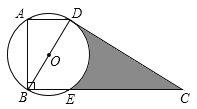
【题目】如图，在梯形ABCD中，，上底AD为，以对角线BD为直径的与CD切于点D，与BC交于点E，且为，则图中阴影部分的面积为____.（结果保留根号）

Answer 1

【答案】

【解析】

连接OE，根据∠ABC=90°，AD=，∠ABD为30°，可得出AB与BD，可证明△OBE为等边三角形，即可得出∠C=30°．阴影部分的面积为直角梯形ABCD的面积-△ABD的面积-△OBE的面积-扇形ODE的面积．

连接OE，过点O作OF⊥BE于点F.

∵∠ABC=90°，,AD=,∠ABD=30°，

∴BD=2，AB=3，AB是直径

∵OB=OE，∠DBC=60°，OF⊥BE，

∴OF=，

∵CD为⊙O的切线，

∴∠BDC=90°，

∴∠C=30°，

∴BC=4，

故答案为.