题目内容
在?ABCD中,AC与BD相交于点O,点E是AB的中点,△ACD的周长为20cm,则△AOE的周长为________cm.
10
分析:根据三角形中位线定理可知OE= AD,根据平行四边形对角线互相平分可知AO=
AD,根据平行四边形对角线互相平分可知AO= AC,根据题意得AE=
AC,根据题意得AE= AB,于是可推出△AOE的周长和△ACD的周长的关系,进而求出△AOE的周长.
AB,于是可推出△AOE的周长和△ACD的周长的关系,进而求出△AOE的周长.
解答: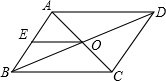 解:如图:
解:如图:
∵O为BD的中点,E为AB的中点,
∴OE为△ABD的中位线,
故OE= AD.
AD.
∵AC为?ABCD的对角线,
∴AO= AC.
AC.
∵E是AB的中点,
所以AE= AB.
AB.
于是EO+AO+AE= AD+
AD+ AC+
AC+ AB=
AB= (AD+AC+AB)=
(AD+AC+AB)= ×20=10.
×20=10.
故答案为10.
点评:此题将平行四边形的性质、三角形中位线定理等知识结合起来,同时需要整体考虑,即将AD+AC+AB看做一个整体解答.
分析:根据三角形中位线定理可知OE=
 AD,根据平行四边形对角线互相平分可知AO=
AD,根据平行四边形对角线互相平分可知AO= AC,根据题意得AE=
AC,根据题意得AE= AB,于是可推出△AOE的周长和△ACD的周长的关系,进而求出△AOE的周长.
AB,于是可推出△AOE的周长和△ACD的周长的关系,进而求出△AOE的周长.解答:
 解:如图:
解:如图:∵O为BD的中点,E为AB的中点,
∴OE为△ABD的中位线,
故OE=
 AD.
AD.∵AC为?ABCD的对角线,
∴AO=
 AC.
AC.∵E是AB的中点,
所以AE=
 AB.
AB.于是EO+AO+AE=
 AD+
AD+ AC+
AC+ AB=
AB= (AD+AC+AB)=
(AD+AC+AB)= ×20=10.
×20=10.故答案为10.
点评:此题将平行四边形的性质、三角形中位线定理等知识结合起来,同时需要整体考虑,即将AD+AC+AB看做一个整体解答.

练习册系列答案
相关题目
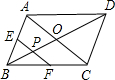 如图,在?ABCD中,AC=6,BD=8,P是对角线BD上的任意一点,过点P作EF∥AC,与?ABCD的两条边分别交于点E,F.设BP=x,EF=y,则下面能大致反映y与x之间关系的图象为( )
如图,在?ABCD中,AC=6,BD=8,P是对角线BD上的任意一点,过点P作EF∥AC,与?ABCD的两条边分别交于点E,F.设BP=x,EF=y,则下面能大致反映y与x之间关系的图象为( )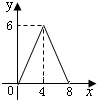
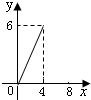
 如图,在?ABCD中,AC、BD相交于点O,点E是AB的中点,OE=5cm,则AD的长是
如图,在?ABCD中,AC、BD相交于点O,点E是AB的中点,OE=5cm,则AD的长是 如图,在?ABCD中,AC为对角线,BE⊥AC,DF⊥AC,E、F为垂足,求证:BE=DF.
如图,在?ABCD中,AC为对角线,BE⊥AC,DF⊥AC,E、F为垂足,求证:BE=DF.