题目内容
14.在一个箱子中有三个分别标有数字1,2,3的材质、大小都相同的小球,从中任意摸出一个小球,记下小球的数字x后,放回箱中并摇匀,再摸出一个小球,又记下小球的数字y.以先后记下的两个数字(x,y)作为点P的坐标.(1)用列表或画树状图,求点P的横坐标与纵坐标的和为4的概率;
(2)求点P落在以坐标原点为圆心、$\sqrt{10}$为半径的圆的内部的概率.
分析 (1)首先根据题意列出表格,然后根据表格即可求得点P坐标的所有可能的结果,然后利用概率公式求解即可;
(2)确定满足条件的点的个数,利用概率公式求解,即可求得答案.
解答 解:(1)根据题意列表如下:
| 1 | 2 | 3 | |
| 1 | (1,1) | (1,2) | (1,3) |
| 2 | (2,1) | (2,2) | (2,3) |
| 3 | (3,1) | (3,2) | (3,3) |
故P(和为4)=$\frac{3}{9}$=$\frac{1}{3}$.
(2)因为点P在以坐标原点为圆心,以$\sqrt{10}$为半径的圆的内部,
所以x2+y2<10,这样的点P有4种形式:(1,1)、(1,2)、(2,1)、(2,2),
所以点P在以坐标原点为圆心,以$\sqrt{10}$为半径的圆的内部的概率P=$\frac{4}{9}$.
点评 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
5.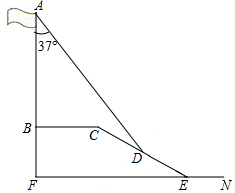 在学习解直角三角形以后,重庆八中数学兴趣小组测量了旗杆的高度.如图,某一时刻,旗杆AB的影子一部分落在平台上的影长BC为6米,落在斜坡上的影长CD为4米,AB⊥BC,同一时刻,光线与旗杆的夹角为37°,斜坡的坡角为30°,旗杆的高度AB约为( )米.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,$\sqrt{3}$≈1.73)
在学习解直角三角形以后,重庆八中数学兴趣小组测量了旗杆的高度.如图,某一时刻,旗杆AB的影子一部分落在平台上的影长BC为6米,落在斜坡上的影长CD为4米,AB⊥BC,同一时刻,光线与旗杆的夹角为37°,斜坡的坡角为30°,旗杆的高度AB约为( )米.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,$\sqrt{3}$≈1.73)
 在学习解直角三角形以后,重庆八中数学兴趣小组测量了旗杆的高度.如图,某一时刻,旗杆AB的影子一部分落在平台上的影长BC为6米,落在斜坡上的影长CD为4米,AB⊥BC,同一时刻,光线与旗杆的夹角为37°,斜坡的坡角为30°,旗杆的高度AB约为( )米.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,$\sqrt{3}$≈1.73)
在学习解直角三角形以后,重庆八中数学兴趣小组测量了旗杆的高度.如图,某一时刻,旗杆AB的影子一部分落在平台上的影长BC为6米,落在斜坡上的影长CD为4米,AB⊥BC,同一时刻,光线与旗杆的夹角为37°,斜坡的坡角为30°,旗杆的高度AB约为( )米.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,$\sqrt{3}$≈1.73)| A. | 10.61 | B. | 10.52 | C. | 9.87 | D. | 9.37 |
4.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
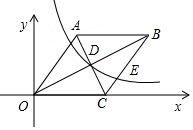 如图,菱形OABC的边OC在x轴正半轴上,点B的坐标为(8,4).
如图,菱形OABC的边OC在x轴正半轴上,点B的坐标为(8,4).
 如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为$\frac{4π}{3}$cm2.(结果保留π)
如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为$\frac{4π}{3}$cm2.(结果保留π)



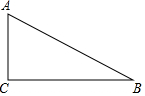 如图,已知Rt△ABC,∠C=90°,AC=3,BC=4.分别以点A、B为圆心画圆.如果点C在⊙A内,点B在⊙A外,且⊙B与⊙A内切,那么⊙B的半径长r的取值范围是8<r<10.
如图,已知Rt△ABC,∠C=90°,AC=3,BC=4.分别以点A、B为圆心画圆.如果点C在⊙A内,点B在⊙A外,且⊙B与⊙A内切,那么⊙B的半径长r的取值范围是8<r<10.