题目内容
在学习扇形的面积公式,同学们得到扇形的面积公式S扇=| n |
| 360 |
| 1 |
| 2 |
| 1 |
| 2 |
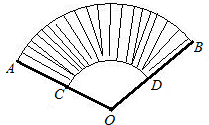 由.
由.
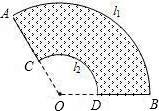
分析:先利用扇形的面积公式和弧长公式分别把扇形AOB和扇形COD的面积和弧长表示出来,扇环的面积=扇形AOB的面积-扇形COD的面积,通过公式变形和线段的和差关系得到扇环面积与扇形的弧长和半径差之间的关系:S=
(C1+C2)d.
| 1 |
| 2 |
解答:解:小明的猜想正确.
理由如下:
设∠AOB=∠COD=n°
扇形AOB的面积S1=
,
扇形COD的面积S2=
,
扇形AOB的弧长C1=
,
扇形COD的弧长C2=
.
所以扇环的面积S=S1-S2=
-
=
(OA2-OC2)
=
(OA-OC)(OA+OC)
=
•(OA+OC)•d
=
(
•OA+
•OC)•d
=
(C1+C2)•d
因此,小明的猜想对.
理由如下:
设∠AOB=∠COD=n°
扇形AOB的面积S1=
| nπ•OA2 |
| 360 |
扇形COD的面积S2=
| nπ•OC2 |
| 360 |
扇形AOB的弧长C1=
| nπ•OA |
| 180 |
扇形COD的弧长C2=
| nπ•OC |
| 180 |
所以扇环的面积S=S1-S2=
| nπ•OA2 |
| 360 |
| nπ•OC2 |
| 360 |
=
| nπ |
| 360 |
=
| nπ |
| 360 |
=
| nπ |
| 360 |
=
| 1 |
| 2 |
| nπ |
| 180 |
| nπ |
| 180 |
=
| 1 |
| 2 |
因此,小明的猜想对.
点评:解决本题首先要牢记扇形的面积公式和弧长公式以及扇形的面积与弧长之间的等量关系.面积公式:S=
;弧长公式:C=
;扇形的面积与弧长之间的等量关系:S=
C•r.
| nπr2 |
| 360 |
| nπr |
| 180 |
| 1 |
| 2 |

练习册系列答案
相关题目
 ,并通过比较扇形面积公式与弧长公式
,并通过比较扇形面积公式与弧长公式 ,得出扇形面积的另一种计算方法S扇形=
,得出扇形面积的另一种计算方法S扇形= ,接着老师让同学们解决两个问题:
,接着老师让同学们解决两个问题: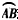 和
和 所在圆的圆心都是点O,
所在圆的圆心都是点O, 的长为l1,
的长为l1, 的长为l2,AC=BD=d,求花坛的面积。
的长为l2,AC=BD=d,求花坛的面积。
 ,类似于三角形面积公式,类比梯形面积公式,他猜想花坛的面积S=
,类似于三角形面积公式,类比梯形面积公式,他猜想花坛的面积S= (l1+l2)d,他的猜想正确吗?如果正确,写出推导过程;如果不正确,请说明理由。
(l1+l2)d,他的猜想正确吗?如果正确,写出推导过程;如果不正确,请说明理由。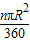 ,并通过比较扇形面积公式与弧长公式l=
,并通过比较扇形面积公式与弧长公式l= ,得出扇形面积的另一种计算方法S扇形=
,得出扇形面积的另一种计算方法S扇形= lR.接着老师让同学们解决两个问题:
lR.接着老师让同学们解决两个问题: lR类似于三角形面积公式;类比梯形面积公式,他猜想花坛的面积S=
lR类似于三角形面积公式;类比梯形面积公式,他猜想花坛的面积S= (l1+l2)d.他的猜想正确吗?如果正确,写出推导过程;如果不正确,请说明理由.
(l1+l2)d.他的猜想正确吗?如果正确,写出推导过程;如果不正确,请说明理由.
 ,并通过比较扇形面积公式与弧长公式l=
,并通过比较扇形面积公式与弧长公式l= ,得出扇形面积的另一种计算方法S扇形=
,得出扇形面积的另一种计算方法S扇形= lR.接着老师让同学们解决两个问题:
lR.接着老师让同学们解决两个问题: lR类似于三角形面积公式;类比梯形面积公式,他猜想花坛的面积S=
lR类似于三角形面积公式;类比梯形面积公式,他猜想花坛的面积S= (l1+l2)d.他的猜想正确吗?如果正确,写出推导过程;如果不正确,请说明理由.
(l1+l2)d.他的猜想正确吗?如果正确,写出推导过程;如果不正确,请说明理由.