题目内容
在学习扇形的面积公式时,同学们推得S扇形=| nπR2 |
| 360 |
| nπR |
| 180 |
| 1 |
| 2 |
问题Ⅰ:求弧长为4π,圆心角为120°的扇形面积.
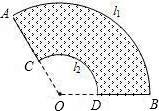
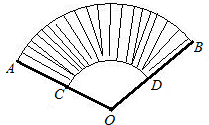
问题Ⅱ:某小区设计的花坛形状如图中的阴影部分,已知AB和CD所在圆心都是点O,弧AB的长为l1,弧CD的长为l2,AC=BD=d,求花坛的面积.
(1)请你解答问题Ⅰ;
(2)在解完问题Ⅱ后的全班交流中,有位同学发现扇形面积公式S扇形=
| 1 |
| 2 |
| 1 |
| 2 |
分析:根据扇形公式之间的关系,结合已知条件推出结果.
解答:解:(1)弧长公式l=
,弧长为4π,圆心角为120°,则可得R=6,
S扇形=
lR=12π.
(2)设大扇形半径为R,小扇形半径为r,圆心角度数为n,则由l=
,得R=
,r=
,
所以图中扇形面积为:
×l1×R-
×l2×r=
l1
-
l2
=
-
)=
(l1+l2)(l1-l2)
=
•
(
R-
r)(l1+l2)
=
•(l1+l2)(R-r)=
(l1+l2)d.
故猜想正确.
| nπR |
| 180 |
S扇形=
| 1 |
| 2 |
(2)设大扇形半径为R,小扇形半径为r,圆心角度数为n,则由l=
| nπR |
| 180 |
| 180l1 |
| nπ |
| 180l2 |
| nπ |
所以图中扇形面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 180l1 |
| nπ |
| 1 |
| 2 |
| 180l2 |
| nπ |
=
| 90 |
| nπ |
| (l | 2 1 |
| l | 2 2 |
| 90 |
| nπ |
=
| 1 |
| 2 |
| 180 |
| nπ |
| nπ |
| 180 |
| nπ |
| 180 |
=
| 1 |
| 2 |
| 1 |
| 2 |
故猜想正确.
点评:本题主要考查了扇形面积公式的应用.

练习册系列答案
相关题目
 由.
由. ,并通过比较扇形面积公式与弧长公式
,并通过比较扇形面积公式与弧长公式 ,得出扇形面积的另一种计算方法S扇形=
,得出扇形面积的另一种计算方法S扇形= ,接着老师让同学们解决两个问题:
,接着老师让同学们解决两个问题: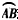 和
和 所在圆的圆心都是点O,
所在圆的圆心都是点O, 的长为l1,
的长为l1, 的长为l2,AC=BD=d,求花坛的面积。
的长为l2,AC=BD=d,求花坛的面积。
 ,类似于三角形面积公式,类比梯形面积公式,他猜想花坛的面积S=
,类似于三角形面积公式,类比梯形面积公式,他猜想花坛的面积S= (l1+l2)d,他的猜想正确吗?如果正确,写出推导过程;如果不正确,请说明理由。
(l1+l2)d,他的猜想正确吗?如果正确,写出推导过程;如果不正确,请说明理由。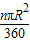 ,并通过比较扇形面积公式与弧长公式l=
,并通过比较扇形面积公式与弧长公式l= ,得出扇形面积的另一种计算方法S扇形=
,得出扇形面积的另一种计算方法S扇形= lR.接着老师让同学们解决两个问题:
lR.接着老师让同学们解决两个问题: lR类似于三角形面积公式;类比梯形面积公式,他猜想花坛的面积S=
lR类似于三角形面积公式;类比梯形面积公式,他猜想花坛的面积S= (l1+l2)d.他的猜想正确吗?如果正确,写出推导过程;如果不正确,请说明理由.
(l1+l2)d.他的猜想正确吗?如果正确,写出推导过程;如果不正确,请说明理由.
 ,并通过比较扇形面积公式与弧长公式l=
,并通过比较扇形面积公式与弧长公式l= ,得出扇形面积的另一种计算方法S扇形=
,得出扇形面积的另一种计算方法S扇形= lR.接着老师让同学们解决两个问题:
lR.接着老师让同学们解决两个问题: lR类似于三角形面积公式;类比梯形面积公式,他猜想花坛的面积S=
lR类似于三角形面积公式;类比梯形面积公式,他猜想花坛的面积S= (l1+l2)d.他的猜想正确吗?如果正确,写出推导过程;如果不正确,请说明理由.
(l1+l2)d.他的猜想正确吗?如果正确,写出推导过程;如果不正确,请说明理由.