题目内容
在直角坐标系中,抛物线 与x轴交于点A,B(点A在点B的左侧),与y轴交于点C。如果点M在y轴的右侧的抛物线上,
与x轴交于点A,B(点A在点B的左侧),与y轴交于点C。如果点M在y轴的右侧的抛物线上, ,那么点M的坐标为
,那么点M的坐标为 
(4,6)或(1,-6)
解析考点:二次函数综合题.
分析:根据抛物线的定义可求出m=2,然后再令y=0,解方程求出A,B两点,再令x=0,求出C点坐标,设出M点坐标,根据它在抛物线上和S△ABO=  S△COB,这两个条件求出M点坐标.
S△COB,这两个条件求出M点坐标.
解:∵y=x2-x-6为抛物线,
∵抛物线y=x2-x-6与x轴交于A,B两点,
令y=0,设方程x2-x-6=0的两根为x1,x2,
∴x1=-2,x2=3,
∴A(-2,0),B(3,0),
设M点坐标为(a,a2-a-6),(a>0)
∵S△AMO= S△COB,
S△COB,
∴ ×AO×yM=
×AO×yM= ×
× ×OC×xB
×OC×xB
∴ ×2×|a2-a-6|=
×2×|a2-a-6|= ×
× ×6×3,
×6×3,
解得,a1=0,a2=1,a3=-3,a4=4,
∵点M在y轴右侧的抛物线上,
∴a>0,
∴a=1或a=4,
a2-a-6=12-1-6=-6,或a2-a-6=42-4-6=6
∴M点坐标为(1,-6)或(4,6).
故答案为:(1,-6)或(4,6).

练习册系列答案
相关题目
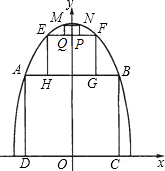 为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:
为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求: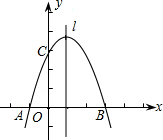 ,B,C三点的抛物的对称轴为直线l,D为对称轴l上一动点.
,B,C三点的抛物的对称轴为直线l,D为对称轴l上一动点.
 为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:
为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求: (2005•杭州)为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:
(2005•杭州)为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求: