Question

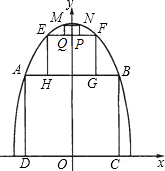为了参加市科技节展览，同学们制造了一个截面为抛物线形的隧道模型，用了三种正方形的钢筋支架．在画设计图时，如果在直角坐标系中，抛物线的函数解析式为y=-x²+c，正方形ABCD的边长和正方形EFGH的边长之比为5：1，求：
（1）抛物线解析式中常数c的值；
（2）正方形MNPQ的边长．

Answer 1

分析：（1）观察各点坐标之间的关系，巧妙设点，减少未知量，由待定系数求出函数表达式，求出c的值；
（2）由题已知条件正方形ABCD的边长和正方形EFGH的边长之比为5：1，求出正方形MNPQ的边长．

解答：解：（1）因各点坐标都关于y轴对称，可以设特殊点坐标．由抛物线的函数解析式为y=-x²+c，
∵AB=BC，
设AB=a，则FE=

a

5

，
又∵抛物线关于y轴对称，
故可设B（

a

2

，a），F（

a

10

，

6

5

a）代入y=-x²+c得：

- a2 4 +c=a - a2 100 +c= 6 5 a

，
即

a= 5 6 c= 145 144

．
抛物线解析式中常数c的值为

145

144

．

（2）∵正方形ABCD的边长和正方形EFGH的边长之比为5：1，即FG=

1

5

BC=

a

5

，
∴F（

a

10

，

a

5

+a）．
设MN=NP=b，则N（

b

2

，b+

6

5

a），
∵a=

5

6

，代入y=-x²+

145

144

∴b+1=-

b2

4

+

145

144

∴正方形MNPQ的边长b=-2+

145

6

．

点评：此题考查二次函数图象上坐标之间的关系，巧妙设点来减少未知量，最后待定系数求出方程的解．