题目内容
如图,长方形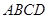 ,设其长
,设其长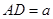 ,宽
,宽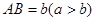 ,在
,在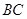 边上选取一点
边上选取一点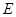 ,将△
,将△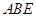 沿
沿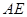 翻折后
翻折后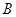 至直线
至直线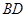 上的
上的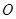 点,若
点,若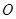 为长方形
为长方形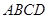 的对称中心,则
的对称中心,则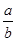 的值是_____________.
的值是_____________.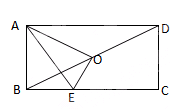
 ,设其长
,设其长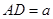 ,宽
,宽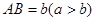 ,在
,在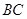 边上选取一点
边上选取一点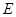 ,将△
,将△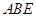 沿
沿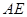 翻折后
翻折后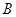 至直线
至直线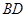 上的
上的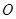 点,若
点,若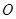 为长方形
为长方形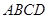 的对称中心,则
的对称中心,则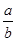 的值是_____________.
的值是_____________.

连接CO,由于O为长方形纸片ABCD的对称中心,A、O、C共线,AC是矩形的对角线,由折叠的性质知可得△ABC三边关系求解.
解答:解:连接CO.

∵O为长方形纸片ABCD的对称中心,A、O、C共线,AC是矩形的对角线,
由折叠的性质知,AC=2AO=2AB=2b,
∴sin∠ACB= =1:2,
=1:2,
∴∠ACB=30°.
cot∠ACB=cot30°=a/b= .
.
故答案为: .
.
解答:解:连接CO.

∵O为长方形纸片ABCD的对称中心,A、O、C共线,AC是矩形的对角线,
由折叠的性质知,AC=2AO=2AB=2b,
∴sin∠ACB=
 =1:2,
=1:2,∴∠ACB=30°.
cot∠ACB=cot30°=a/b=
 .
.故答案为:
 .
.
练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目

 的两条对角线相交于点
的两条对角线相交于点 ,
, ,则矩形的对角线
,则矩形的对角线 的长是( )
的长是( )


 ABCD中,BC=7厘米,CD=5厘米,∠D=50°,
ABCD中,BC=7厘米,CD=5厘米,∠D=50°,

 ,小⊙O的直径CD=2,连接AC、AD、BD、BC,AD、CB分别交小⊙O于E、F.
,小⊙O的直径CD=2,连接AC、AD、BD、BC,AD、CB分别交小⊙O于E、F.
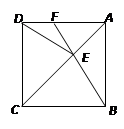
 ∠B=20°,则∠ADE=_____________.
∠B=20°,则∠ADE=_____________.