题目内容
已知A,B,C为⊙O上顺次三点且∠AOC=150°,那么∠ABC的度数是________.
75°或105°
分析:由于点B的位置不能确定,故应分两种情况进行讨论.
解答: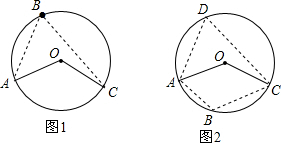 解:当A、B、C三点如图1所示时,
解:当A、B、C三点如图1所示时,
连接AB、BC,
∵∠AOC与∠ABC是同弧所对的圆心角与圆周角,
∴∠ABC= ∠AOC=
∠AOC= ×150°=75°;
×150°=75°;
当A、B、C三点如图2所示时,连接AB、BC,
作 对的圆周角∠ADC,
对的圆周角∠ADC,
∵∵∠AOC与∠ADC是同弧所对的圆心角与圆周角,
∴∠ADC= ∠AOC=
∠AOC= ×150°=75°,
×150°=75°,
∵四边形ABCD是⊙O的内接四边形,
∴∠ABC=180°-∠ADC=180°-75°=105°.
故答案为:75°或105°.
点评:本题考查的是圆周角定理,在解答此题时要注意分类讨论,不要漏解.
分析:由于点B的位置不能确定,故应分两种情况进行讨论.
解答:
 解:当A、B、C三点如图1所示时,
解:当A、B、C三点如图1所示时,连接AB、BC,
∵∠AOC与∠ABC是同弧所对的圆心角与圆周角,
∴∠ABC=
 ∠AOC=
∠AOC= ×150°=75°;
×150°=75°;当A、B、C三点如图2所示时,连接AB、BC,
作
 对的圆周角∠ADC,
对的圆周角∠ADC,∵∵∠AOC与∠ADC是同弧所对的圆心角与圆周角,
∴∠ADC=
 ∠AOC=
∠AOC= ×150°=75°,
×150°=75°,∵四边形ABCD是⊙O的内接四边形,
∴∠ABC=180°-∠ADC=180°-75°=105°.
故答案为:75°或105°.
点评:本题考查的是圆周角定理,在解答此题时要注意分类讨论,不要漏解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 (1997•贵阳)已知:如图,CD为⊙O的直径,CD⊥AB,M为垂足,DM=2cm,弦AB=8cm,则⊙O的半径为
(1997•贵阳)已知:如图,CD为⊙O的直径,CD⊥AB,M为垂足,DM=2cm,弦AB=8cm,则⊙O的半径为 P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.