题目内容
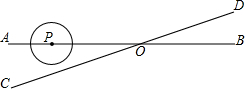直线AB，CD相交于点O，∠AOC=30°，半径为1cm的⊙P的圆心在射线OA上，开始时，PO=6cm，如果⊙P以1cm/秒的速度沿由A向B的方向移动，那么当⊙P的运动时间t（单位：秒）满足什么条件时，⊙P与直线CD相切？考点：直线与圆的位置关系
专题：动点型
分析：分别利用⊙P在O点左边以及右边时分别求出相切时的时间即可．
解答：
解：如图所示：当∠AOC=30°，半径为1cm的⊙P与直线CD相切，
则P′E=1cm，则OP′=2cm，
故PP′=4cm，则当⊙P的运动时间为4s时，⊙P与直线CD相切，
当∠DOB=30°，半径为1cm的⊙P与直线CD相切，
则P″F=1cm，则OP″=2cm，
故PP″=8cm，则当⊙P的运动时间为8s时，⊙P与直线CD相切，
综上所述：当⊙P的运动时间t为4秒或8秒时，⊙P与直线CD相切．
解：如图所示：当∠AOC=30°，半径为1cm的⊙P与直线CD相切，则P′E=1cm，则OP′=2cm，
故PP′=4cm，则当⊙P的运动时间为4s时，⊙P与直线CD相切，
当∠DOB=30°，半径为1cm的⊙P与直线CD相切，
则P″F=1cm，则OP″=2cm，
故PP″=8cm，则当⊙P的运动时间为8s时，⊙P与直线CD相切，
综上所述：当⊙P的运动时间t为4秒或8秒时，⊙P与直线CD相切．
点评：此题主要考查了直线与圆的位置关系，利用分类讨论得出是解题关键．
练习册系列答案
相关题目
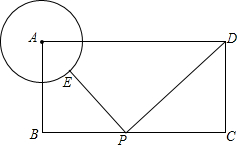如图，矩形ABCD中，AB=2，BC=3，以A为圆心，1为半径画⊙A，E是圆⊙A上一动点，P是BC上一动点，则PE+PD最小值是（ ）
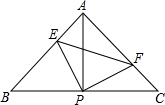如图，已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC中点，两边PE、PF分别交AB、AC于点E、F，给出以下四个结论：①AE=CF；②△EPF是等腰直角三角形；③S四边形AEPF=
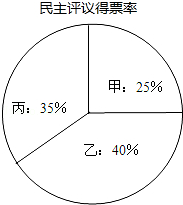某单位欲从内部公开选拔一名管理人员，对甲、乙、丙三名候选人进行了笔试面试两项测试，三人的测试成绩如表：
如图，AB、AC分别与⊙O相切于B，C两点，连接OA交⊙O于点D．求证：D是△ABC的内心．
如图，在△ABC中，∠ACB=90°，AC=BC，AD⊥CE，BE⊥CE，D、E为垂足．求证：DE+BE=CE．