题目内容
如图,三角形ABC的两个顶点B、C在圆上,顶点A在圆外,AB、AC分别交圆于E、D两点,连结EC、BD.
(1)求证:ΔABD∽ΔACE;
(2)若ΔBEC与ΔBDC的面积相等,试判定三角形ABC的形状.

(1)证明:因为![]() 弧ED所对的圆周角相等,所以∠EBD=∠ECD,…………………2分
弧ED所对的圆周角相等,所以∠EBD=∠ECD,…………………2分
又因为∠A=∠A,所以△A![]() BD∽ΔACE.……………………………………………4分
BD∽ΔACE.……………………………………………4分
(2)法1:因为S△BEC=S△BCD,
S△ACE=S△ABC-S△BEC,S△ABD=S△ABC一S△BCD,………………………………6分
所以S△ACE=S△ABD,
又由(1)知△ABD∽ΔACE,
所以对应边之比等于1,……………………………………………………………8分
所以AB=AC,即三角形ABC为等腰三角形.……………………………………9分
法2:因为ΔBEC与ΔBCD的面积相等,有公共底边BC,所以高相等,
即E、D两点到BC距离相等,所以ED‖BC,……………………………………6分
所以∠BCE=∠CED,
又因为∠CED=∠CBD,
所以∠BCE=∠CBD,………………………………………………………………8分![]()
由(1)知△ABD∽ΔACE,
所以∠ABD=∠ACE,
所以∠ABC=∠ACB,
即三角形ABC为等腰三角形. ……………………………………………………9分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
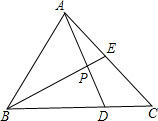 如图,三角形ABC的面积为1,BD:DC=2:1,E为AC的中点,AD与BE相交于P,那么四边形PDCE的面积为
如图,三角形ABC的面积为1,BD:DC=2:1,E为AC的中点,AD与BE相交于P,那么四边形PDCE的面积为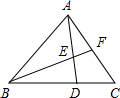 如图,三角形ABC的面积是30平方厘米,AE=ED、BD=
如图,三角形ABC的面积是30平方厘米,AE=ED、BD= (2012•潍坊)如图,三角形ABC的两个顶点B、C在圆上,顶点A在圆外,AB、AC分别交圆于E、D两点,连接EC、BD.
(2012•潍坊)如图,三角形ABC的两个顶点B、C在圆上,顶点A在圆外,AB、AC分别交圆于E、D两点,连接EC、BD.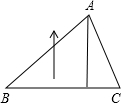 如图,三角形ABC的底边BC长3厘米,BC边上的高是2厘米,将三角形以每秒3厘米的速度沿高的方向向上移动2秒,这时,三角形扫过的面积是多少平方厘米( )
如图,三角形ABC的底边BC长3厘米,BC边上的高是2厘米,将三角形以每秒3厘米的速度沿高的方向向上移动2秒,这时,三角形扫过的面积是多少平方厘米( )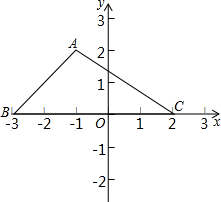 如图,三角形ABC的顶点坐标分别是A(-1,2),B(-3,0),C(2,0),求△ABC的面积.
如图,三角形ABC的顶点坐标分别是A(-1,2),B(-3,0),C(2,0),求△ABC的面积.