题目内容
9.将一个圆心角为120°,半径为6cm的扇形围成一个圆锥的侧面,则所得圆锥的高为4$\sqrt{2}$cm.分析 设圆锥的底面圆的半径为r,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到=$\frac{120•π•6}{180}$,解得r=2,然后利用勾股定理计算圆锥的高.
解答 解:设圆锥的底面圆的半径为r,
根据题意得2πr=$\frac{120•π•6}{180}$,解得r=2,
所以圆锥的高=$\sqrt{{6}^{2}-{2}^{2}}$=4$\sqrt{2}$(cm).
故答案为4$\sqrt{2}$.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.据2015年1月24日《高青工作》报道,高青县2014年财政收入11.4亿元,比上年增长8.27%.将11.4亿用科学记数法表示为( )
| A. | 1.14×107 | B. | 1.14×108 | C. | 1.14×109 | D. | 1.14×1010 |
20.16的平方根是( )
| A. | ±4 | B. | 4 | C. | -4 | D. | ±8 |
1.直线y=$\frac{1}{2}$x+b与直线y=-2x+2的交点不可能在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
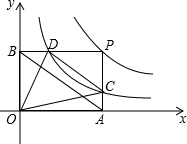 如图,P(m,n)是函数y=$\frac{6}{x}$(x>0)的图象上的一个动点,过点P分别作PA⊥x轴于A、PB⊥y轴于B,PA、PB分别与函数y=$\frac{2}{x}$(x>0)的图象交于点C、D,连接AB、CD.
如图,P(m,n)是函数y=$\frac{6}{x}$(x>0)的图象上的一个动点,过点P分别作PA⊥x轴于A、PB⊥y轴于B,PA、PB分别与函数y=$\frac{2}{x}$(x>0)的图象交于点C、D,连接AB、CD. 如图,正方形ABCD的对角线BD长为2$\sqrt{2}$,若直线满足:(1)点D到直线的距离为1;(2)A、C两点到直线的距离相等,则符合题意的直线的条数为( )
如图,正方形ABCD的对角线BD长为2$\sqrt{2}$,若直线满足:(1)点D到直线的距离为1;(2)A、C两点到直线的距离相等,则符合题意的直线的条数为( )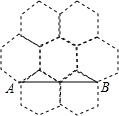 蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有10.
蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有10.