题目内容
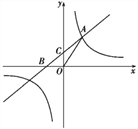
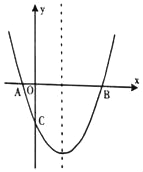
【题目】如图，抛物线y=ax2+bx﹣
经过A（﹣1，0），B（5，0）两点．
（1）求此抛物线的解析式；
（2）在抛物线的对称轴上有一点P，使得PA+PC的值最小时，求△ABP的面积；
（3）点M为x轴上一动点，在抛物线上是否存在一点N，使以A，C，M，N四点构成的四边形为平行四边形？若存在，直接写出点N的坐标；若不存在，请说明理由．
【答案】（1）y=
x2﹣2x﹣
；（2）
；（3）符合条件的点N的坐标为（4，﹣）、（2+
，）或（2﹣，）．
【解析】分析：(1)、利用待定系数法求出函数解析式；(2)、连接BC，求出BC的函数解析式，直线BC与对称轴的交点就是点P；(3)、分两种情况求出点N的坐标，即点N在x轴下方和点N在x轴上方，根据两种情况分别画出图形，从而得出答案．
详解：（1）把A（﹣1，0），B（5，0）代入y=ax2+bx﹣，
得到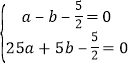
，解得：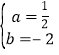
， 即抛物线的解析式为y=x2﹣2x﹣；
（2）∵抛物线的解析式为：y=x2﹣2x﹣， ∴其对称轴为直线x=﹣
=2，
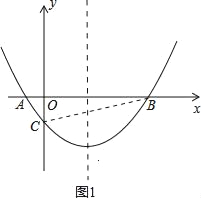
连接BC，如图1所示， ∵B（5，0），C（0，﹣）， ∴设直线BC的解析式为y=kx+b（k≠0），
∴
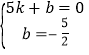，解得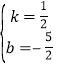
， ∴直线BC的解析式为y=x﹣，
当x=2时，y=1﹣=﹣
， ∴P（2，﹣）， S△ABP=×6×=；
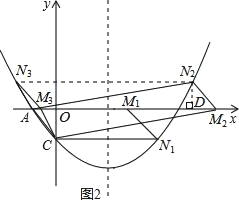
（3）存在，如图2所示，
①当点N在x轴下方时， ∵抛物线的对称轴为直线x=2，C（0，﹣）， ∴N1（4，﹣）；
②当点N在x轴上方时，过点N作ND垂直x轴于点D， 在△AND与△MCO中，
∠NAD=∠CMO，AN=CM, ∠AND=∠MCO， ∴△AND≌△MCO（ASA），
∴ND=OC=，即N点的纵坐标为， ∴x2﹣2x﹣=， 解得：x=2±，
∴N2（2+，），N3（2﹣，），
综上所述，符合条件的点N的坐标为（4，﹣）、（2+，）或（2﹣，）．
