题目内容
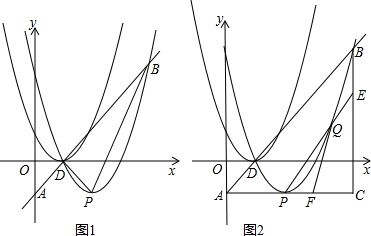
如图,抛物线c1:y=ax2-2ax-c与x轴交于A、B,且AB=6,与y轴交于C(0,-4 ).【小题1】求抛物线c1的解析式;
【小题2】问抛物线c1上是否存在P、Q(点P在点Q的上方)两点,使得以A、C、P、Q为顶点的四边形为直角梯形,若存在,求P、Q两点坐标;若不存在,请说明理由;
【小题3】抛物线c2与抛物线c1关于x轴对称,直线x=m分别交c1、c2于D、E两点,直线x=n分别交c1、c2于M、N两点,若四边形DMNE为平行四边形,试判断m和n间的数量关系,并说明理由.

【小题1】

【小题2】存在,P、Q的坐标分别为(5,
 ),(3,
),(3, )或(-5,
)或(-5, ),(3,-
),(3,- )
)【小题3】m+n=0,m≠0,n≠0.解析:
此题是二次函数的综合题,涉及到求解析式、平行四边的性质等。
(1)解:把C(0.-4)代入抛物线的解析式得:c=4,
∴y=ax2-2ax-4,
∵AB=6,
所以
 =
=
解得:a=0(舍去),a=
 ,
,∴

(2)解:有两种情况:①当∠PAC=∠ACQ=90°时如图(1),连接AQ,设Q(x,x2-x-4),
由勾股定理得:AQ2=AC2+CQ2,
代入得:

解得:x=0(舍去),x=3,
当x="3" 时,x2-x-4=-
 ,
,∴Q(3,
 ),
),同法可求P的坐标是(5,
 );
);②当∠ACQ=∠PQC=90°时如图(2),与①解法类似可求出Q的坐标是(3,-
 ),P的坐标是(-5,
),P的坐标是(-5, );
);故存在,P、Q的坐标分别为(5,
 ),(3,
),(3, )或(-5,
)或(-5, ),(3,-
),(3,- ).
).(3)答:m和n间的数量关系是m+n=0,且m≠0,n≠0.
理由是:∵抛物线c2与抛物线c1关于x轴对称,
∴两抛物线的形状相同,开口方向相反,且都关于Y轴对称,
∵直线x=m分别交c1、c2于D、E两点,直线x=n分别交c1、c2于M、N两点,四边形DMNE为平行四边形,
∴直线m n垂直于X轴(m∥n),DE=MN,DE与 MN关于Y轴对称,
∴m+n=0,m≠0,n≠0.

练习册系列答案
相关题目
 16、如图,抛物线C1:y=x2-4x的对称轴为直线x=a,将抛物线C1向上平移5个单位长度得到抛物线C2,则图中的两条抛物线、直线x=a与y轴所围成的图形(图中阴影部分)的面积为
16、如图,抛物线C1:y=x2-4x的对称轴为直线x=a,将抛物线C1向上平移5个单位长度得到抛物线C2,则图中的两条抛物线、直线x=a与y轴所围成的图形(图中阴影部分)的面积为 26、已知:如图,抛物线C1,C2关于x轴对称;抛物线C1,C3关于y轴对称.抛物线C1,C2,C3与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线C1,C2,C3的顶点.HN垂直于x轴,垂足为N,且|OE|>|HN|,|AB|≠|HG|
26、已知:如图,抛物线C1,C2关于x轴对称;抛物线C1,C3关于y轴对称.抛物线C1,C2,C3与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线C1,C2,C3的顶点.HN垂直于x轴,垂足为N,且|OE|>|HN|,|AB|≠|HG|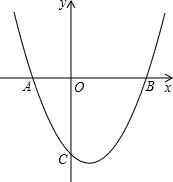 如图,抛物线c1:y=ax2-2ax-c与x轴交于A、B,且AB=6,与y轴交于C(0,-4 ).
如图,抛物线c1:y=ax2-2ax-c与x轴交于A、B,且AB=6,与y轴交于C(0,-4 ).