Question

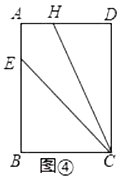
【题目】对给定的一张矩形纸片进行如下操作：先沿折叠，使点落在边上(如图①)，再沿折叠，这时发现点恰好与点重合(如图②)

(1)根据以上操作和发现，则____；

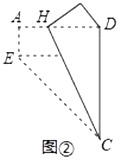
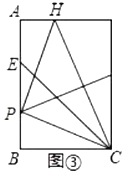
(2)将该矩形纸片展开，如图③，折叠该矩形纸片，使点与点重合，折痕与相交于点，再将该矩形纸片展开．

求证：；

Answer 1

【答案】(1)；(2)证明见解析.

【解析】

(1)依据是等腰直角三角形，即可得到，由图②，可得，而，即可得到，即；(2)由翻折可得，，即，依据勾股定理可得，进而得出，再根据，∠A=∠B=90°，即可得到，进而得到；

(1)由图①，可得，

又∵，

∴是等腰直角三角形，

∴，即，

由图②，可得，

∵，

∴，

∴.

故答案为：

(2)设，则，，

∴，

如图③，连接，则，

∵，，

∴，

∴，

设，则，由翻折可得，，即，

∴，

即

解得，即，

又∵，，

∴，

∴，

又∵中，，

∴，

∴.