Question

【题目】如图，把半径为的沿弦折叠，经过圆心，则阴影部分的面积为__________．（结果保留）

Answer 1

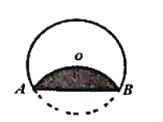
【答案】

【解析】

过O作OD⊥AB于D，交劣弧AB于E，根据勾股定理求出AD，根据垂径定理求出AB，分别求出扇形AOB和三角形AOB的面积，即可得出答案．

过O作OD⊥AB于D，交劣弧AB于E，如图：

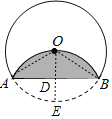
∵把半径为2的⊙O沿弦AB折叠，经过圆心O，

∴OD=DE=1，OA=2，

∵在Rt△ODA中，sinA==，

∴∠A=30°，

∴∠AOE=60°，

同理∠BOE=60°，

∴∠AOB=60°+60°=120°，

在Rt△ODA中，由勾股定理得：AD===，

∵OD⊥AB，OD过O，

∴AB=2AD=2，

∴阴影部分的面积S=S扇形AOB-S△AOB=-×2×1=-，

故答案为：-．