题目内容
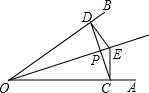如图，已知E是∠AOB的平分线上的一点，EC⊥OA，ED⊥OB，垂足分别为C、D，你能得到哪些结论？并证明你的结论．分析：根据角平分线上的点到角的两边的距离相等可得DE=CE，再利用“HL”证明△OCE和△ODE全等，根据全等三角形对应边相等可得OC=OD．
解答：解：结论：OP垂直平分CD．
∵E是∠AOB的平分线上的一点，EC⊥OA，ED⊥OB，
∴DE=CE，
在△OCE和△ODE中，
，
∴△OCE≌△ODE（HL），
∴OC=OD，
∵OE是∠AOB的平分线，
∴OP垂直平分CD．
∵E是∠AOB的平分线上的一点，EC⊥OA，ED⊥OB，
∴DE=CE，
在△OCE和△ODE中，
|
∴△OCE≌△ODE（HL），
∴OC=OD，
∵OE是∠AOB的平分线，
∴OP垂直平分CD．
点评：本题考查了角平分线上的点到角的两边的距离相等的性质，全等三角形的判定与性质，以及等腰三角形三线合一的性质．
练习册系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
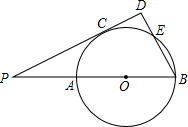如图，已知PAB是⊙O的割线，AB为⊙O的直径，PC为⊙O的切线，C为切点，BD⊥PC于点D，交⊙O于点E，PA=AO=OB=1．
OD交圆O于点D，过点B作AB的垂线交AD的延长线于点E，若线段AO、OD的长是一元二次方程x2-3x+2=0的两根．
（2013•瑶海区一模）如图，已知A是反比例函数
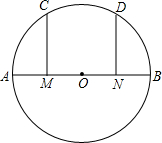如图，已知AB是⊙O的直径，M，N分别是AO，BO的中点，CM⊥AB，DN⊥AB．求证：