题目内容
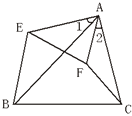
如图,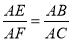 ,∠1=∠2,则对于结论: ①△ABE∽△ACF; ②△ABC∽△AEF ③
,∠1=∠2,则对于结论: ①△ABE∽△ACF; ②△ABC∽△AEF ③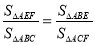 ④
④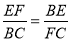 ,其中正确的结论的个数是( )
,其中正确的结论的个数是( )
A.1 B.2 C.3 D.4
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
如图,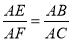 ,∠1=∠2,则对于结论: ①△ABE∽△ACF; ②△ABC∽△AEF ③
,∠1=∠2,则对于结论: ①△ABE∽△ACF; ②△ABC∽△AEF ③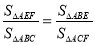 ④
④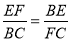 ,其中正确的结论的个数是( )
,其中正确的结论的个数是( )

A.1 B.2 C.3 D.4
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案