题目内容
如图,抛物线 与y轴交于点C(0,-4),与x轴交于点A,B,且B点的坐标为(2,0)
与y轴交于点C(0,-4),与x轴交于点A,B,且B点的坐标为(2,0)
(1)求该抛物线的解析式;
(2)若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值;
(3)若点D为OA的中点,点M是线段AC上一点,且△OMD为等腰三角形,求M点的坐标.
解:(1)把点C(0,-4),B(2,0)分别代入 中,
中,
得 ,解得
,解得 。
。
∴该抛物线的解析式为 。
。
(2)令y=0,即 ,解得x1=-4,x2=2。
,解得x1=-4,x2=2。
∴A(﹣4,0),S△ABC= AB•OC=12。
AB•OC=12。
设P点坐标为(x,0),则PB=2﹣x。
∵PE∥AC,∴∠BPE=∠BAC,∠BEP=∠BCA。∴△PBE∽△ABC。
∴ ,即
,即 ,化简得:
,化简得: 。
。
∴
 。
。
∴当x=﹣1时,S△PCE的最大值为3。
(3)△OMD为等腰三角形,可能有三种情形:
①当DM=DO时,如图①所示,
∵DO=DM=DA=2,
∴∠OAC=∠AMD=45°。∴∠ADM=90°。
∴M点的坐标为(-2,-2)。
②当MD=MO时,如图②所示,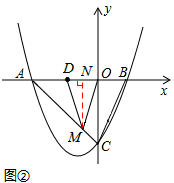
过点M作MN⊥OD于点N,则点N为OD的中点,
∴DN=ON=1,AN=AD+DN=3,
又△AMN为等腰直角三角形,∴MN=AN=3。
∴M点的坐标为(-1,-3)。
③当OD=OM时,
∵△OAC为等腰直角三角形,
∴点O到AC的距离为 ×4=
×4= ,即AC上的点与点O之间的最小距离为
,即AC上的点与点O之间的最小距离为 。
。
∵ >2,∴OD=OM的情况不存在。
>2,∴OD=OM的情况不存在。
综上所述,点M的坐标为(-2,-2)或(-1,-3)。
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ),线段AB的垂直平分线交x轴于点C,交AB于点D.
),线段AB的垂直平分线交x轴于点C,交AB于点D.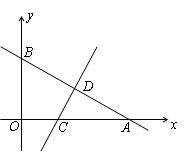
 ,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.
,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.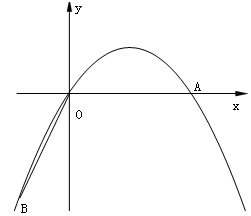
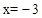 与抛物线相交于第三象限的点M,与x轴相交于点N,且
与抛物线相交于第三象限的点M,与x轴相交于点N,且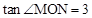 。
。
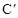 ,抛物线
,抛物线 与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3).
与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3).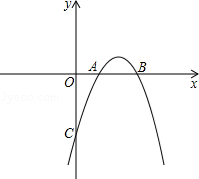
 中,A、B为x轴上两点,C、D为y轴上的两点,经
中,A、B为x轴上两点,C、D为y轴上的两点,经 ),点M是抛物线C2:
),点M是抛物线C2: (
( <0)的顶点.
<0)的顶点.
 (a>0),点A(n,y1)、B(n+1,y2)、C(n+2,y3)都在这个二次函数的图象上,其中n为正整数.
(a>0),点A(n,y1)、B(n+1,y2)、C(n+2,y3)都在这个二次函数的图象上,其中n为正整数.