题目内容
如图,在直角坐标系中,点A的坐标为( ,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.
,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.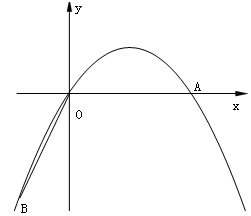
(1)请直接写出点B的坐标;
(2)求经过A、O、B三点的抛物线的解析式;
(3)如果点P是(2)中的抛物线上的动点,且在x轴的上方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.
(1)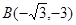 (2)
(2)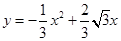
(3)当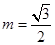 ,即
,即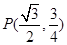 时,
时,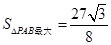 .
.
解析试题分析:(1)过 作y轴的垂线,垂足为E,在直角三角形
作y轴的垂线,垂足为E,在直角三角形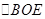 中求解;(2)设抛物线的解析式为
中求解;(2)设抛物线的解析式为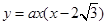 ,因为
,因为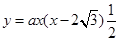 过
过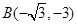 ,
,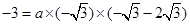 ,
,
可得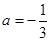 ,从而求经过A、O、B三点的抛物线的解析式
,从而求经过A、O、B三点的抛物线的解析式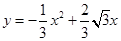 .
.
(3)作PN⊥x轴,垂足为M,交AB于点N,设P(m,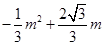 ).
).
则M(m,0),已知A(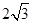 ,0),
,0),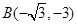 .
.
求得直线AB的函数解析式为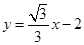 ,所以,
,所以,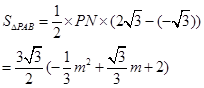
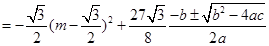 ,根据抛物线的性质得出最大值.
,根据抛物线的性质得出最大值.
试题解析:(1) 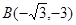
(2)设抛物线的解析式为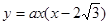
∵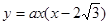 过
过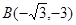
∴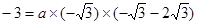
∴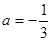
∴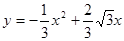 4分
4分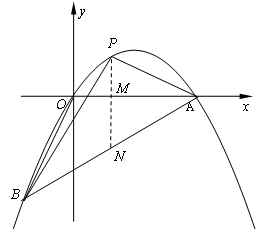
(3)作PN⊥x轴,垂足为M,交AB于点N,设P(m,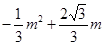 ) 5分
) 5分
则M(m,0),
∵A( ,0),
,0),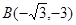
∴直线AB的函数解析式为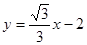
∴N(m,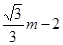 ) 6分
) 6分
∴PN=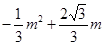 -(
-(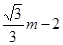 )=
)= 7分
7分
∴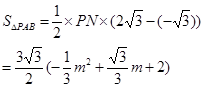 8分
8分
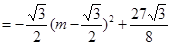 9分
9分
当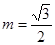 ,即
,即 时, 11分
时, 11分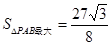 . 12分
. 12分
考点:1.借解直角三角形求点的坐标.2.待定系数法求解析式.3.二次函数的性质.

练习册系列答案
相关题目
 有两个不同的实数根,方程
有两个不同的实数根,方程 也有两个不同的实数根,且其两根介于方程
也有两个不同的实数根,且其两根介于方程 与直线
与直线 交于点A 、B,与y轴交于点C.
交于点A 、B,与y轴交于点C.
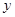 (件)与销售单价
(件)与销售单价 (元)之间的关系近似满足一次函数:
(元)之间的关系近似满足一次函数: .
. (元),当销售单价定为多少元时,每月可获得最大利润?
(元),当销售单价定为多少元时,每月可获得最大利润?
 多36 m2时,求x的值.
多36 m2时,求x的值.
 与y轴交于点C(0,-4),与x轴交于点A,B,且B点的坐标为(2,0)
与y轴交于点C(0,-4),与x轴交于点A,B,且B点的坐标为(2,0)

 )在直线MG上。问:当m为何值时,在抛物线C3上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形?
)在直线MG上。问:当m为何值时,在抛物线C3上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形?