ЬтФПФкШн
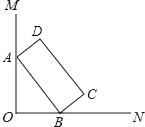
ЁОЬтФПЁПШчЭМ1ЃЌЁїABCжаЃЌЁЯACB=90ЁуЃЌAC=BC=6ЃЌMЕудкБпACЩЯЃЌЧвCM=2ЃЌЙ§MЕузїACЕФДЙЯпНЛABБпгкEЕуЃЌЖЏЕуPДгЕуAГіЗЂбиACБпЯђMЕудЫЖЏЃЌЫйЖШЮЊ1ИіЕЅЮЛ/УыЃЌЕБЖЏЕуPЕНДяMЕуЪБЃЌдЫЖЏЭЃжЙ.СЌНгEPЁЂECЃЌЩшдЫЖЏЪБМфЮЊtЃЎдкДЫЙ§ГЬжа:
ЃЈ1ЃЉЕБt=1ЪБЃЌЧѓEPЕФГЄЖШЃЛ
ЃЈ2ЃЉЕБtЮЊКЮжЕЪБЃЌЁїEPCЪЧЕШбќШ§НЧаЮЃП
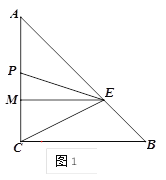
ЃЈ3ЃЉШчЭМ2ЃЌШєЕуNЪЧЯпЖЮMEЩЯвЛЕуЃЌЧвMN=3ЃЌЕуQЪЧЯпЖЮAEЩЯвЛЖЏЕуЃЌСЌНгPQЁЂPNЁЂNQЕУЕНЁїPQNЃЌЧыжБНгаДГіЁїPQNжмГЄЕФзюаЁжЕ.

ЁОД№АИЁПЃЈ1ЃЉ5ЃЛЃЈ2ЃЉЕБt=1Лђ2ЛђЃЈ6-2![]() ЃЉЪБЃЌЁїPECЪЧЕШбќШ§НЧаЮЃЛЃЈ3ЃЉЁїPQNжмГЄЕФзюаЁжЕЪЧ
ЃЉЪБЃЌЁїPECЪЧЕШбќШ§НЧаЮЃЛЃЈ3ЃЉЁїPQNжмГЄЕФзюаЁжЕЪЧ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЦНааЯпЕФаджЪСаГіБШР§ЪНЃЌЧѓГіEPЃЛ
ЃЈ2ЃЉЗжEP=ECЁЂPC=PEЁЂCP=CEШ§жжЧщПіЃЌИљОнЕШбќШ§НЧаЮЕФИХФюЁЂЙДЙЩЖЈРэМЦЫуМДПЩЃЛ
ЃЈ3ЃЉзїЕуNЙигкACЕФЖдГЦЕуNЁфЃЌЙигкABЕФЖдГЦЕуNЁфЁфЃЌСЌНгNЁфNЁфЁфНЛACгкPЃЌНЛABгкQЃЌСЌНгNЁфЁфEЃЌИљОнЙДЙЩЖЈРэЧѓГіNЁфNЁфЁфЃЌЕУЕНД№АИЃЎ
НтЃКЃЈ1ЃЉЁпЁЯACB=90ЁуЃЌEMЁЭACЃЌ
ЁрEMЁЮBCЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрME=4ЃЌ
ЕБt=1УыЪБЃЌAP=1ЃЌ
дђPM=3ЃЌ
ЁрEP=![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБEP=ECЪБЃЌPM=MCЃЌ
Ёр4-t=2ЃЌ
НтЕУЃЌt=2ЃЌ
ЕБPC=PEЪБЃЌЃЈ4-tЃЉ2+42=ЃЈ6-tЃЉ2ЃЌ
НтЕУЃЌt=1ЃЌ
ЕБCP=CEЪБЃЌ22+42=ЃЈ6-tЃЉ2ЃЌ
НтЕУЃЌt1=6+![]() ЃЈЩсШЅЃЉЃЌt2=6-
ЃЈЩсШЅЃЉЃЌt2=6-![]() ЃЌ
ЃЌ
ЕБt=1Лђ2ЛђЃЈ6-2![]() ЃЉЪБЃЌЁїPECЪЧЕШбќШ§НЧаЮЃЛ
ЃЉЪБЃЌЁїPECЪЧЕШбќШ§НЧаЮЃЛ
ЃЈ3ЃЉзїЕуNЙигкACЕФЖдГЦЕуNЁфЃЌЙигкABЕФЖдГЦЕуNЁфЁфЃЌСЌНгNЁфNЁфЁфНЛACгкPЃЌНЛABгкQЃЌСЌНгNЁфЁфEЃЌдђЁїPQNМДЮЊжмГЄзюаЁЕФШ§НЧаЮЃЛ

гЩЬтвтЕУЃЌNЁфE=7ЃЌNЁфЁфE=NE=1ЃЌ
ЁпMEЁЮBCЃЌ
ЁрЁЯAEN=ЁЯB=45ЁуЃЌ
ЁрЁЯNЁфЁфEN=90ЁуЃЌ
ЁрNЁфNЁфЁф=![]() ЃЌ
ЃЌ
дђЁїPQNжмГЄЕФзюаЁжЕЪЧ![]() ЃЎ
ЃЎ