题目内容
 67、将一张长方形纸ABCD的两个角按如图所示方式折叠,且BE与EC的一部分重合,请问,∠α与∠β是有什么关系的两个角,并说明理由.
67、将一张长方形纸ABCD的两个角按如图所示方式折叠,且BE与EC的一部分重合,请问,∠α与∠β是有什么关系的两个角,并说明理由.分析:由折叠的性质知,∠B′EF=∠BEF,∠GEC′=∠CEG,则这四个角的和为180°进而求解得∠α+∠β的值.
解答:解:互余(即∠α+∠β=90°),
理由:由折叠可知∠B′EF=∠α,∠GEC′=∠β,
而∠BEC=180°,
所以∠α+∠FEB′+∠GEC+∠GEC′=180°,
即2∠α+2∠β=180°,
所以∠α+∠β=90°.
理由:由折叠可知∠B′EF=∠α,∠GEC′=∠β,
而∠BEC=180°,
所以∠α+∠FEB′+∠GEC+∠GEC′=180°,
即2∠α+2∠β=180°,
所以∠α+∠β=90°.
点评:本题利用了:①折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;②一个平角是180度.

练习册系列答案
相关题目

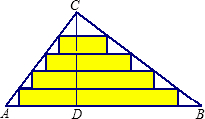 如图,△ABC是一张直角三角形彩色纸,AC=30cm,BC=40cm.
如图,△ABC是一张直角三角形彩色纸,AC=30cm,BC=40cm.

