题目内容
 如图,在?ABCD中,DE平分∠ADC,AD=6,BE=2,则?ABCD的周长是
如图,在?ABCD中,DE平分∠ADC,AD=6,BE=2,则?ABCD的周长是考点:平行四边形的性质,等腰三角形的判定与性质
专题:
分析:根据角平分线的定义以及两直线平行,内错角相等求出∠CDE=∠CED,再根据等角对等边的性质可得CE=CD,然后利用平行四边形对边相等求出CD、BC的长度,再求出?ABCD的周长.
解答:解:∵DE平分∠ADC,
∴∠ADE=∠CDE,
∵?ABCD中,AD∥BC,
∴∠ADE=∠CED,
∴∠CDE=∠CED,
∴CE=CD,
∵在?ABCD中,AD=6,BE=2,
∴AD=BC=6,
∴CE=BC-BE=6-2=4,
∴CD=AB=4,
∴?ABCD的周长=6+6+4+4=20.
故答案为:20.
∴∠ADE=∠CDE,
∵?ABCD中,AD∥BC,
∴∠ADE=∠CED,
∴∠CDE=∠CED,
∴CE=CD,
∵在?ABCD中,AD=6,BE=2,
∴AD=BC=6,
∴CE=BC-BE=6-2=4,
∴CD=AB=4,
∴?ABCD的周长=6+6+4+4=20.
故答案为:20.
点评:本题考查了平行四边形对边平行,对边相等的性质,角平分线的定义,等角对等边的性质,是基础题,准确识图并熟练掌握性质是解题的关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
下列计算正确的是( )
| A、2a+a2=3a3 |
| B、a6÷a2=a3 |
| C、(a2)3=a6 |
| D、3a2-2a=a2 |
下列长度的各组线段首尾相接能构成三角形的是( )
| A、3cm、5cm、8cm |
| B、3cm、5cm、6cm |
| C、3cm、3cm、6cm |
| D、3cm、5cm、10cm |
 如图是一辆汽车油箱里剩油量y(L)与行驶时间x(h)的图象,根据图象回答下列问题:
如图是一辆汽车油箱里剩油量y(L)与行驶时间x(h)的图象,根据图象回答下列问题: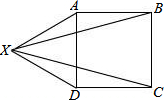 如图,ABCDXA表示一条环形高速公路,X表示一座水库,B,C表示两个大市镇,已知ABCD是一个正方形,XAD是一个等边三角形,假设政府要铺设两条输水管XB和XC,从水库向B,C两个市镇供水,那么着两水管的夹角∠BXC=
如图,ABCDXA表示一条环形高速公路,X表示一座水库,B,C表示两个大市镇,已知ABCD是一个正方形,XAD是一个等边三角形,假设政府要铺设两条输水管XB和XC,从水库向B,C两个市镇供水,那么着两水管的夹角∠BXC=