��Ŀ����
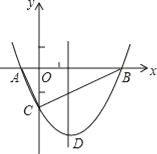
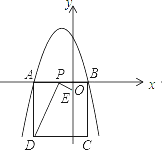
����Ŀ�����κ���y=![]() ��ͼ����x�ύ�ڵ�A�͵�B����ABΪ����x���·���������ABCD����P��x����һ���㣬����DP������P��DP�Ĵ�����y�ύ�ڵ�E��
��ͼ����x�ύ�ڵ�A�͵�B����ABΪ����x���·���������ABCD����P��x����һ���㣬����DP������P��DP�Ĵ�����y�ύ�ڵ�E��
��1�����m��ֵ�������A����B�����꣮
��2������P���߶�AO����P����A��O�غϣ����˶����δ�ʱ���߶�OE�ij������ֵ�����������ֵ��
��3���Ƿ���������ĵ�P��ʹ��PED�ǵ��������Σ������ڣ��������P�����꼰��ʱ��PED��������ABCD�ص����ֵ�������������ڣ���˵�����ɣ�
���𰸡���1��m=��2��A����3��0����B��1��0������2��PΪAO�е�ʱ��OE�����ֵΪ![]() ����3�����ڣ�������.
����3�����ڣ�������.
��������
��1�����ö��κ����Ķ������m��֪������y=0���ɵó���A��B���ꣻ
��2����PA=t��-3��t��0������OP=3-t����ͼ1��֤����DAP�ס�POE���������Ʊȵõ�OE=-![]() ��Ȼ�����ö��κ��������ʽ�����⣻
��Ȼ�����ö��κ��������ʽ�����⣻
��3�����ۣ�����P��y�����ʱ����ͼ2��DE��AB��G�㣬֤����DAP�ա�POE�õ�PO=AD=4����PA=1��OE=1��������ƽ���߷��߶γɱ������������AG=![]() �������S��DAG���ɵõ���ʱ��PED��������ABCD�ص����ֵ��������P����y���Ҳ�ʱ����ͼ3��DE��AB��G�㣬DP��BC�ཻ��Q��ͬ���ɵ���DAP�ա�POE����PO=AD=4��PA=7��OE=7��������ƽ���߷��߶γɱ������������OG��BQ��Ȼ�����S�ı���DGBQ�õ���ʱ��PED��������ABCD�ص����ֵ����������P�͵�A�غ�ʱ����E�ͺ͵�O�غϣ���ʱ����PED���ǵ��������Σ�
�������S��DAG���ɵõ���ʱ��PED��������ABCD�ص����ֵ��������P����y���Ҳ�ʱ����ͼ3��DE��AB��G�㣬DP��BC�ཻ��Q��ͬ���ɵ���DAP�ա�POE����PO=AD=4��PA=7��OE=7��������ƽ���߷��߶γɱ������������OG��BQ��Ȼ�����S�ı���DGBQ�õ���ʱ��PED��������ABCD�ص����ֵ����������P�͵�A�غ�ʱ����E�ͺ͵�O�غϣ���ʱ����PED���ǵ��������Σ�
��1���߶��κ���y=��m��1��![]() ��6x+9��
��6x+9��
��m2+m=2��m��1��0��
��m=��2��
����κ�������ʽΪy=��3x2��6x+9��
��y=0��
��0=��3x2��6x+9��
��x=1��x=��3��
��A����3��0����B��1��0����
��2����PA=t����3��t��0������OP=3��t��
��DP��PE��
���DPA=��PEO��
���DAP�ס�POE��
��![]() ����
����![]() ��
��
��OE=��![]() t2+
t2+![]() t=��
t=��![]() ��t��
��t��![]() ��2+
��2+![]() ��
��
�൱t=![]() ʱ��OE�����ֵ��
ʱ��OE�����ֵ��
��PΪAO�е�ʱ��OE�����ֵΪ![]() ��
��
��3�����ڣ�
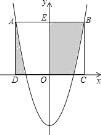
����P��y�����ʱ����ͼ1��DE��AB��G�㣬
��PD=PE����DPE=90����
���DAP�ա�POE��
��PO=AD=4��
��PA=1��OE=1��
��AD��OE��
��![]() =4��
=4��
��AG=![]() ��
��
��S��DAG=![]() ��
��![]() ��4=
��4=![]() ��
��
��P������Ϊ����4��0������ʱ��PED��������ABCD�ص����ֵ����Ϊ��![]() ��P����y���Ҳ�ʱ����ͼ2��DE��AB��G�㣬DP��BC�ཻ��Q��ͬ���ɵ���DAP�ա�POE��
��P����y���Ҳ�ʱ����ͼ2��DE��AB��G�㣬DP��BC�ཻ��Q��ͬ���ɵ���DAP�ա�POE��
��PO=AD=4��
��PA=7��OE=7��
��AD��OE��
��![]() ��
��
��OG=![]() ��
��
ͬ���ɵ�BQ=![]() ��
��
��S�ı���DGBQ=![]() ����
����![]() +1����4+
+1����4+![]() ��4��
��4��![]() =
=![]()
�൱��P������Ϊ��4��0��ʱ����ʱ��PED��������ABCD�ص����ֵ����Ϊ![]() ��
��
����P�͵�A�غϣ���ʱ����E�͵�O�غϣ���DP��OP����ʱ����PDE���ǵ��������Σ�

 A�ӽ��� ϵ�д�
A�ӽ��� ϵ�д� ȫ�Ų��Ծ�ϵ�д�
ȫ�Ų��Ծ�ϵ�д�