题目内容
如果△ABC中，∠A+∠B=∠C-10°，则△ABC是
钝角
钝角
三角形．分析：根据三角形内角和定理可知∠A+∠B+∠C=180°，再与∠A+∠B=∠C-10°联立即可得出∠C的度数，进而得出结论．
解答：解：∵△ABC中，∠A+∠B+∠C=180°
∴∠A+∠B=180°-∠C，
∵∠A+∠B=∠C-10°，
∴180°-∠C=∠C-10°，解得∠C=98.5°，
∴△ABC是钝角三角形．
故答案为：钝角．
∴∠A+∠B=180°-∠C，
∵∠A+∠B=∠C-10°，
∴180°-∠C=∠C-10°，解得∠C=98.5°，
∴△ABC是钝角三角形．
故答案为：钝角．
点评：本题考查的是三角形内角和定理，熟知三角形的内角和等于180°是解答此题的关键．
练习册系列答案
天天向上口算本系列答案
相关题目
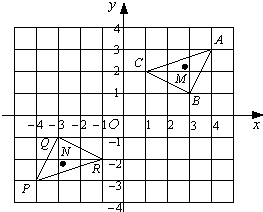15、如图，△PQR是△ABC经过某种变换后得到的图形．如果△ABC中任意一点M的坐标为（a，b），那么它的对应点N的坐标为如果△ABC中，∠A：∠B：∠C=1：2：3，那么BC：AC：AB的值是（ ）
| A、1：2：3 | ||
| B、3：2：1 | ||
C、1：
| ||
D、1：2：
|
